Estudio de las Pruebas Diagnósticas
Introducción
Decidir si un sujeto está enfermo es el paso previo a una acción posterior: tratar, esperar y asegurarse, o no tratar. Supónganse las cuatro mediciones de presión arterial siguientes tomadas por el mismo observador en el mismo sujeto: 160/96, 150/92, 155/86 y 170/98. La media de la presión sistólica es 159 y la de la diastólica, 93. Según la primera y la cuarta mediciones, el sujeto se identificaría como hipertenso, no así si se tienen en cuenta las otras dos, ni tampoco si se atiende a la media de las estimaciones. La hipertensión arterial es un concepto que se deriva de una estimación. En sí es una variable continua y los puntos de corte que la Organización Mundial de la Salud (OMS) ha establecido para su identificación (160/95 y 140/90) son fruto de un acuerdo, tras comprobar que unas cifras altas aumentan el riesgo de presentar procesos cardiovasculares. Esto subraya que la valoración de una entidad a través de una prueba está sometida a variabilidad y que la definición de la entidad no es evidente para todos, incluido el propio sujeto, que con esa tensión puede encontrarse clínicamente bien.
Para evitar errores, es preciso conocer el grado de variación y su origen. La variación se puede deber al acto de la medición o a las diferencias biológicas. No se insistirá en las fuentes de variación biológica, porque la formación médica gira en torno a ella.
Variación del acto de la medición
Al estructurar el proceso de medición se aprecian dos grandes fuentes de variabilidad: la reproducibilidad, o grado en que concuerdan dos o más mediciones sobre la misma muestra, y la validez, o grado en que una medición coincide con la verdad. Se ilustrarán con un ejemplo. Suponga que se quiere acertar en una diana con una carabina. Si los disparos se agrupan como en la figura 15-1a, se encuentran en el cuadrante superior izquierdo y bastante próximos. El tirador no es válido, ya que se desvía hacia arriba y a la izquierda, pero es reproducible, da en el mismo sitio. Es probable que cuando compruebe cómo ha tirado, mejore en la siguiente tanda; el sesgo, cuando se conoce, se puede corregir. Suponga ahora que la agrupación de los disparos es la de la figura 15-1b. No es un tirador reproducible. Es más, la falta de reproducibilidad es tan grande que dificulta la apreciación de la validez: no se puede observar la existencia de alguna tendencia a desviarse del centro de la diana. La reproducibilidad es un paso previo para la determinación de la validez. Los disparos pueden presentarse como en la figura 15-1c, no tan agrupados como en la figura 15-1a, pero mejor que en la figura 15-1b; este tirador es más reproducible que el de la figura 15-1b, pero menos que el de la figura 15-1a; también se aprecia que se desvía hacia arriba y a la derecha, lo que refleja falta de validez. En este caso, la falta de reproducibilidad no impide valorar la validez. Por último, la diana puede reflejar el aspecto de la figura 15-1d; es un tirador reproducible y válido.
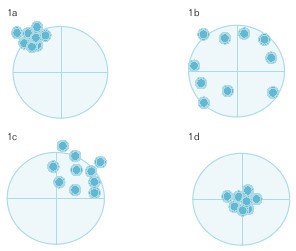
Estudio de la reproducibilidad
Recibe también los nombres de concordancia, acuerdo y fiabilidad. Se concede menos valor a la reproducibilidad que a la validez en el diagnóstico. Al actuar así se ignoran dos hechos. En primer lugar, que para poder valorar la validez hay que tener antes reproducibilidad. Por ejemplo, en el pasado, a la psiquiatría se le achacó una falta de concordancia en el diagnóstico. Si lo que para un profesional es una neurosis, para otro es una psicosis, y viceversa, los resultados de una investigación no se podrán generalizar. Para profundizar en el tema será necesario avanzar en el consenso de lo que se entiende para cada proceso, con independencia de que sea real o no. En segundo lugar, hay muchos procesos en los que el diagnóstico no tiene un referente absoluto y se basa en un consenso: fiebre reumática, colon irritable, etc. Es más, el referente por excelencia, la anatomía patológica, se basa en el consenso. Éste tiene como finalidad esencial aumentar la reproducibilidad en ausencia de un criterio de referencia. Todo consenso es fruto del conocimiento de un momento; por lo tanto, cuando avance éste habrá que modificar el consenso. En estas situaciones la reproducibilidad es el parámetro central de estudio.
Existen esencialmente dos tipos de reproducibilidad:
- intraobservador, o grado de coincidencia que mantiene un observador consigo mismo, y
- entre observadores, o grado de coincidencia entre dos o más observadores.
Los procedimientos de valoración son los mismos para ambos tipos. En la valoración de la reproducibilidad se distinguirán dos situaciones: variable categórica y continua. Las primeras suelen ser más importantes, ya que la realización de pruebas diagnósticas se hace con la finalidad de tomar decisiones (está el sujeto enfermo o no), por lo que muchas variables continuas en algún momento se categorizan.
Reproducibilidad de variables categóricas
Inicialmente se valorará la situación más sencilla, una característica puede estar presente o ausente. Teniendo en cuenta que la tabla 15-1 son pares de observaciones, el acuerdo específico en lo positivo será el número de concordancias en los resultados positivos dividido por el total de observaciones positivas: Po+ = 2a / (2a + b + c). Se procederá de igual manera con el acuerdo específico en lo negativo, dividiendo el total de concordancias negativas por el total de observaciones negativas: Po– = 2d / (2d + b + c). Po+ y Po– oscilan entre 0 y 1. El acuerdo total, en lo positivo y en lo negativo, dividiendo el total de observaciones concordantes por el total de observaciones: Po = (a + d) / (a + b + c + d).
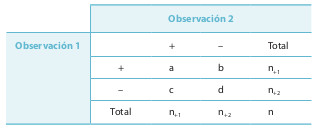
Las asimetrías entre los pares discordantes indican que hay sesgo. Si b < c, o viceversa, una de las medidas tiene tendencia a dar más resultados positivos que otra, o que la segunda da más resultados negativos que la primera, o las dos anteriores. La falta de un criterio de verdad impide decidir cuál de las tres alternativas anteriores es correcta. Se puede calcular el índice de sesgo de McNemar: SMcN = (c – b) / (c + b).
Suponga los datos contemplados en el ejemplo 1 de la tabla 15-2. Se pueden calcular los acuerdos específicos y el total:
Po+ = 30 / (30 + 10 + 10) = 30 / 50 = 0,6; Po– = 130 / (130 + 10 + 10) = 130 / 150 = 0,87; Po = 80 / (15 + 10 + 10 + 65) = 80 / 100 = 0,80; SMcN = (10 – 10) / (10 + 10) = 0 / 20 = 0.
Suponga ahora los datos del ejemplo 2 de la tabla 15-2. Se pueden calcular nuevamente los índices mencionados que darán los valores Po+ = 0 (no hay concordancia en la detección del proceso), Po– = 0,89 y Po = 0,8. Los valores de Po en los dos ejemplos son iguales, pero es muy distinto el valor de Po+ (0 y 60%). El acuerdo global es una prueba en la que influyen varios hechos, y no debería ser nunca el único parámetro que deba utilizarse, debe ir acompañado de los acuerdos específicos.
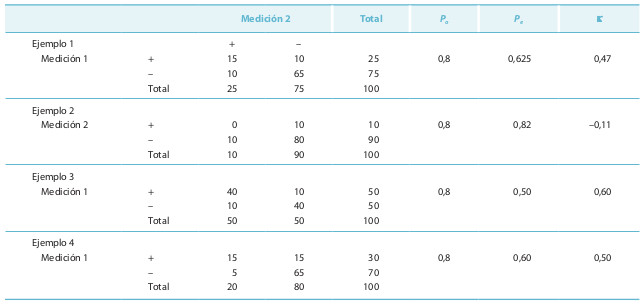
Dos observaciones hechas sobre la misma muestra pueden coincidir por azar. La prueba de kappa (κ) o test de Cohen es una medida de acuerdo global que tiene en cuenta la coincidencia esperada por el azar y que, además, pueda ser generalizable a la existencia de más de dos categorías en una prueba diagnóstica. Se partirá de una distribución semejante a la de la tabla 15-3a. Con los números absolutos se puede construir una tabla de probabilidades, dividiendo cada casilla por el total de la muestra (n) (tabla 15-3b).
La prueba de κ mide la mejora de la concordancia observada (Po) sobre la esperada (Pe), referida a la máxima mejora alcanzable sobre la concordancia esperada, donde Pe = Σ pk+ × p+k y Po = Σ pkk.
La mejora de la concordancia observada sobre la esperada es Po – Pe . La máxima mejora posible sobre la concordancia esperada es 1 – Pe , ya que la máxima concordancia observada posible sería la unidad. De esta manera: κ = (Po – Pe) / (1 – Pe). El límite inferior puede ser negativo; el límite superior máximo es 1. El error estándar de κ es:
$$EE \left (κ \right) = \frac{\sqrt{P_{e} + P_{e}^{2 - \sum P_{κ} \times P_{+κ} \times \left (P_{κ+} + P_{+κ} \right)}}}{\left (1 - P_{e} \right) \sqrt{n}}$$
Con el error estándar se puede calcular un intervalo de confianza a IC κ = κ ± zα/2 × EE(κ).
Los datos anteriores se ilustran con un ejemplo numérico (ejemplo 1). Estos datos absolutos se transforman en una tabla de probabilidad, y para ello el valor numérico de cada casilla se divide por el total (100): Po = 0,15 + 0,65 = 0,8 y Pe = 0,25 × 0,25 + 0,75 × 0,75 = 0,625. Si Po es elevada, también lo es Pe . La concordancia observada mejora en 0,175 a la esperada, sobre un máximo posible de 0,375 (= 1 – 0,625): κ = (0,8 – 0,625) / (1 – 0,625) = 0,175 / 0,375 = 0,47.
Para interpretar el nivel de concordancia según la prueba de κ, se han publicado una serie de directrices: a) Para Fleiss, >0,75, excelente; 0,4-0,75, moderado, y <0,4, pobre, y b) para Landis y Koch, >0,8, muy bueno: 0,61-0,8, bueno; 0,41-0,6, moderado; 0,21-0,4, bajo, y <0,21, pobre.
La κ está sometida a varios influjos que no dependen de la concordancia. Como puede comprobarse en los cuatro ejemplos de la tabla 15-2, con una misma concordancia observada de 0,80 el valor de k varía entre –0,11 y 0,60. Un mayor desequilibrio entre el número de positivos y negativos dados por cada medición, la frecuencia de enfermedad o los sesgos en las discordancias pueden influir en el valor de k.
Por ello, ante un cierto valor de concordancia global esperada se puede hacer un análisis de sensibilidad del k en función de la simetría de la tabla. Se han desarrollado formulaciones que facilitan estas estimaciones. Las fórmulas para estimar los valores máximo y mínimo de κ para un valor observado de concordancia son: κmáx = P²o / [(1 – Po)² + 1] y κmín = (Po – 1) / (1 + Po). En el caso del ejemplo de la tabla 15-2, con una concordancia global del 80%, κmáx = 0,8 2 / [(1 – 0,8)² + 1] = 0,62 y κmín = (0,8 – 1) / (1 + 0,8) = –0,11.
En general, se aconseja que, además de comunicar los resultados de κ, se expresen Po+ y Po– .
κ ponderada
Cuando la prueba de κ se aplica a variables politómicas ordinales (ej. el estadio de una enfermedad), la prueba asigna el mismo grado de desacuerdo a la diferencia en un nivel que a la diferencia en dos. Este inconveniente se soslaya mediante el uso de κ ponderada. En él se asignan pesos a cada diferencia. La ecuación para estimar la κ es idéntica a la anterior, pero trabajando con proporciones de concordancia esperadas y observadas ponderadas por el esquema asignado de pesos: κ = (Pow – Pew) /( 1 – Pew), donde la proporción observada y esperada de concordancias ponderada se estima ponderando cada casilla de la tabla por el peso ωij asignado a cada casilla: Pow = 1 / n Σ Σ ωij nij y Pew = 1 / n² Σ Σ ωij ni+ n+j.
Para asignar la ponderación, los métodos más aceptados son: a) el esquema cuadrático, ωij = 1 – (i – j)² / (r – 1)² , donde r es el número de categorías e i y j son el rango de las categorías para cada casilla (filas y columnas, respectivamente, 1 ≤ i, j ≤ r), y b) la ponderación por los errores absolutos: ωij = 1 – |i – j| / (r – 1), donde |i – j| indica la diferencia entre ambos en valor absoluto. Se suele preferir el sistema cuadrático de pesos. Los criterios de ponderación deben oscilar entre 1 (hay acuerdo) y 0 (máximo grado de desacuerdo).
Problemas clínicos en el uso de κ
κ tiende a disminuir su valor conforme el número de las categorías es mayor. Una alternativa que debe considerarse en estos casos es la de hacer múltiples comparaciones de dos, enfrentando cada categoría con el resto. La κ ponderada es más elevada que la normal.
La influencia de los desequilibrios entre resultados positivos y negativos está en cierto modo gobernada por la prevalencia subyacente de la condición en estudio. Esto tiene derivaciones clínicas importantes. Si se tiene en cuenta que prevalencias de enfermedad superiores al 50% suelen ser poco frecuentes, una κ realizada en un área de frecuencia más elevada de la enfermedad será mayor que la obtenida en un área de baja prevalencia. Esto quiere decir que dos pruebas de κ serán comparables si las circunstancias subyacentes de frecuencia de la enfermedad son similares, con independencia de otros detalles metodológicos. Por ejemplo, dos médicos que contrasten su interpretación de los signos electrocardiográficos (ECG) de infarto de miocardio en una muestra de pacientes con alta frecuencia de infarto obtendrán un valor de κ superior que el que se aprecie por dos médicos que interpreten ECG en pacientes de bajo riesgo. Y no se debe a que manejen mejor el ECG, sino al simple hecho de que la frecuencia de infarto es diferente en las dos situaciones.
También tiene interés la influencia de la prevalencia para justificar otros hechos. Se ha comprobado, por ejemplo, que los cardiólogos son más concordantes que los internistas sobre el significado del perfil enzimático para sugerir el diagnóstico de infarto agudo de miocardio (IAM). Se debe a que los cardiólogos piensan con más frecuencia en IAM que los internistas, ya que el IAM es más frecuente proporcionalmente entre los pacientes que atienden; los internistas, por el espectro más amplio de pacientes a los que asisten, probablemente piensen en otras causas que puedan justificar un perfil enzimático alterado. En conclusión, es más fácil que coincidan los más especializados que los que atienden un mayor espectro de enfermos.
Como resultado de los hechos anteriores, puede comprobarse que la concordancia en el cribado de una enfermedad suele ser inferior a la obtenida en el medio clínico, por la menor frecuencia de la enfermedad subyacente.
Reproducibilidad de variables continuas
Toda variable continua puede categorizarse y entonces se procedería calculando los parámetros mencionados, pero la categorización normalmente supone una pérdida de información. En estos casos pueden utilizarse otros procedimientos. No hay que usar los coeficientes de correlación porque no indica que dos o más procedimientos coincidan. Se puede obtener una correlación perfecta, con ausencia completa de coincidencia. El segundo gran problema que se deriva del uso de los coeficientes de correlación surge de la regresión a la media. Por ejemplo, se puede comparar el peso declarado por los sujetos con el encontrado en la báscula. La correlación será menor que 1 y, teniendo en cuenta el principio de regresión a la media, se esperará encontrar que el peso medio declarado (variable dependiente) por los sujetos obesos sea menor que el encontrado en la báscula (variable independiente), y lo contrario sucederá con los muy delgados; esto significa que los obesos tienden a infraestimar su peso, mientras que los delgados lo sobrestiman. Por la misma razón (ρ < 1), si se toma como variable independiente al peso declarado y como dependiente el peso en la báscula, los sujetos con valores declarados elevados de peso tienden a pesar menos en báscula y lo contrario sucede con los muy delgados. Se alcanzarían en este caso las conclusiones contrarias: los obesos exageran su peso y los delgados lo subestiman.
Esto puede aplicarse a la comparación de dos métodos de medición cualesquiera.
El procedimiento que debe aplicarse para analizar la concordancia en la medición de una variable continua se basa en la determinación de dos nuevas variables: la diferencia entre las determinaciones y la media de ambas. Con estas nuevas variables se pueden realizar varias pruebas estadísticas: el coeficiente de correlación intraclase o la t de Student para muestras emparejadas. Existen equivalencias entre los métodos mencionados, por lo que sólo se explicará el más sencillo, la t de Student. Para ello se crea una variable (y), la diferencia entre las mediciones de los dos observadores. Después se calcula la diferencia media (ym) y el error estándar de ésta [ee(y)]. Con los valores anteriores se puede calcular un estadístico t con (n – 1) grados de libertad: t = ym / ee(y), o se puede construir un intervalo de confianza de la diferencia media, ym ± t1-α/2 × ee(y). Si la diferencia media es estadísticamente significativa o el intervalo de confianza no incluye el 0, esto sugiere la presencia de sesgo: uno de los observadores mide de más, otro de menos, o ambos.
En 1983, Altman y Bland sugirieron la representación gráfica de las diferencias entre los sujetos (x1 – x2) en el eje de ordenadas frente a la respuesta media en cada sujeto [(x1 + x2) / 2] en las abscisas. Una concordancia perfecta entre los dos observadores producirá una línea paralela al eje de las abscisas con una ordenada igual a 0. Con esta representación también se puede comprobar si la diferencia entre observadores es función del valor de la medición.
Validez de una prueba diagnóstica
Es el grado en el que los resultados de una medición corresponden al fenómeno real que se mide (la «verdad»). La medición de la prueba problema se compara con un estándar aceptado.
Parámetros de validez interna
Sensibilidad (S)
Indica la probabilidad que tiene una prueba diagnóstica de dar resultados positivos entre los sujetos enfermos: S = VP / (VP + FN) (tabla 15-4). Una sensibilidad de 0,8 u 80% indica que la prueba da un resultado positivo en el 80% de los que tienen el proceso en estudio.
| Criterio de verdad | |||
|---|---|---|---|
| Prueba | + | VP | FP |
| - | FN | VN | |
Persigue detectar el proceso. Por ello, en general se quiere una prueba sensible cuando la enfermedad es grave, no puede permanecer ignorada y es tratable, o cuando no sea tratable y exista la posibilidad de transmisión a otros (ej. el VIH). También se requiere una alta sensibilidad cuando se desea descartar una hipótesis en el proceso diagnóstico. Las pruebas que se aplican en el cribado de una enfermedad (población sana) requieren una alta sensibilidad (ej. en el cáncer de mama).
Especificidad (E)
Indica la probabilidad que tiene una prueba diagnóstica de dar resultados negativos entre los sujetos que no tienen la enfermedad problema: E = VN / (VN + FP). Una especificidad de 0,9 o 90% significa que una prueba tiene la capacidad de dar resultados negativos en el 90% de los que no tienen la condición problema. La especificidad busca confirmar al que no tiene un proceso como tal (disminuir los falsos positivos). Se desea una prueba muy específica cuando: a) la enfermedad es seria y difícilmente tratable, y b) el hecho de saber que no se tiene la enfermedad posee una importancia sanitaria y psicológica. Estas condiciones se cumplen, por ejemplo, en el caso del VIH o la esclerosis en placas.
La sensibilidad y la especificidad se consideran parámetros de validez interna de una prueba, esto es, que deberían ser estables si las condiciones en las que se valoran fueran absolutamente uniformes e idénticas. Pero no es así, y se observa que cuando sale una nueva prueba al mercado y se analiza, hay una gran variabilidad entre los diferentes estudios. Muchas son las variables que pueden justificar esta heterogeneidad. Descartando el error aleatorio y otros, las que más pueden influir son las características de la medición y la muestra sobre la que se realiza. Es obvio que si las condiciones de valoración no son las mismas (diferente aparato, criterio no idéntico, etc), los parámetros cambian. Con respecto a la muestra, en ella se incluyen enfermos y no enfermos.
En los primeros, la sensibilidad se relaciona de manera directa con el estadio de la enfermedad: cuanto más avanzado es, mayor es la sensibilidad. En el grupo de no enfermos pueden haberse incluido sujetos sanos, donde es más probable que la prueba dé un resultado negativo, que sujetos con otras enfermedades en las que se aplica el diagnóstico diferencial con la que interesa.
Tal y como se han definido, no parece haber ninguna relación entre la sensibilidad y la especificidad; una se valora en los sujetos que tienen el proceso en estudio, y la otra, en los que no la tienen. Para apreciar si esto es así, suponga que quiere estudiar la capacidad diagnóstica de la tonometría ocular en el diagnóstico del glaucoma. Los resultados son los que se esquematizan en la figura 15-2.
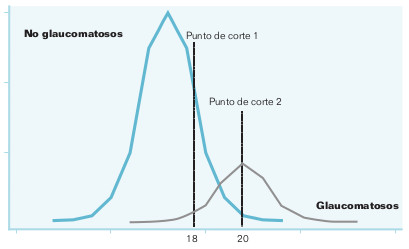
Hay dos curvas de presiones oculares, la de los no glaucomatosos y la de los glaucomatosos. Existe un solapamiento de las curvas porque hay individuos con glaucoma normotensional y, por otra parte, también hay sujetos que nunca tendrán glaucoma a pesar de unos valores elevados de presión ocular. Inicialmente se establece como criterio diagnóstico una cifra de presión ocular de 18 mmHg. El área por debajo de la curva de los sanos situada a la derecha del punto de corte representa a los falsos positivos (FP), ya que en realidad no están enfermos y, sin embargo, la prueba indica que lo están. El área que queda a la izquierda del punto de corte por debajo de la curva de los sanos representa a los verdaderos negativos (VN) (la prueba dice que no, y así es). Con respecto a la curva de los glaucomatosos, el área a la izquierda del punto de corte y por debajo de la curva representa a los falsos negativos (FN), ya que de verdad presentan glaucoma y, sin embargo, la prueba da un resultado negativo; por el contrario, el área a la derecha del punto de corte por debajo de esta curva representa a los verdaderos positivos (VP).
Suponga ahora que el criterio diagnóstico no es 18 sino 20 mmHg. Esto supone que el número de FP disminuye y el de VN aumenta, es decir, la especificidad aumenta. Por el contrario, la sensibilidad disminuye, ya que el número de FN aumenta mientras que los VP disminuyen. Si se utilizara un criterio aún más restrictivo, un valor de presión ocular superior a 20 mmHg, la especificidad aumentaría mientras que la sensibilidad disminuiría aún más. Lo contrario sucedería cuando se utiliza un criterio diagnóstico más laxo.
Los datos anteriores muestran que, por regla general, existe una relación inversa entre la sensibilidad y la especificidad de una prueba diagnóstica. En variables continuas, la elección del punto depende de los objetivos que se persigan.
Conforme el criterio es más exigente, menor es la sensibilidad y mayor es la especificidad. Estos resultados son lógicos, ya que cada vez es más difícil que los pacientes cumplan el criterio (hay más FN), pero es más improbable que un no enfermo los cumpla (disminuyen los FP).
El criterio diagnóstico se establece en función de las necesidades del investigador. En el caso de la figura 15-2, si está interesado en que no se le escapen muchos glaucomatosos, sacrificará la especificidad y tendrá muchos FP.
Si se va a aplicar la tonometría ocular en un estudio comunitario, hay muchos menos glaucomatosos que no enfermos en la población, y por eso la repercusión de un alto número de FP puede alterar mucho los resultados de una investigación. Ésta es la razón de que en los estudios de población normalmente se exija a las pruebas una mayor especificidad que sensibilidad, aunque la elección también depende de las características de la prueba diagnóstica definitiva.
La relación entre sensibilidad y especificidad puede representarse gráficamente, la curva ROC (receiver operating characteristic, denominación frecuente en aparatos electrónicos, en radar, etc., pero que no tiene significado en medicina). En una curva ROC (fig. 15-3), la sensibilidad se representa en el eje de las ordenadas y el complementario de la especificidad (1 – E o proporción de FP) en el eje de las abscisas. Esto tiene como sentido que el área que queda por debajo de la curva represente los diagnósticos correctos (VN y VP), mientras que el área que queda por encima de ella son los FP y FN. Una forma sencilla de calcular el área bajo la curva es mediante la U de Mann-Whitney. El área es igual a la probabilidad de que un sujeto aleatorio con la enfermedad tenga un valor más elevado de medición que una persona aleatoria sin la enfermedad.
La curva ROC presenta varias utilidades:
- ofrecer una impresión gráfica de las relaciones que mantienen entre sí la sensibilidad y la especificidad;
- facilitar la elección de puntos de corte en los criterios diagnósticos de una prueba (hay técnicas matemáticas que permiten conocer los puntos de inflexión de la curva, y ésos suelen ser los primeros candidatos);
- conocer la capacidad diagnóstica global de una prueba diagnóstica a lo largo de todo su espectro de valores, y
- comparar pruebas diagnósticas de manera gráfica y estadística para decidir cuál es la mejor.
Por ejemplo, en la figura 15-3 se han representado cuatro curvas diagnósticas. Está claro que (a) es mejor que (b), porque en todo momento el área cubierta por la curva (a) es mayor que la de la (b). Si se preguntara cuál es la peor de las cuatro curvas, podría pensarse que (d), ya que el área bajo ella es claramente más pequeña que la de las otras tres. Si se piensa, la representación de la curva (d) a lo mejor no es adecuada. Si se le da la vuelta y se considera como positivo lo que otrora fuera negativo, y viceversa, la situación sería muy diferente. Por eso, la mejor de las curvas es (d), aunque erróneamente representada.
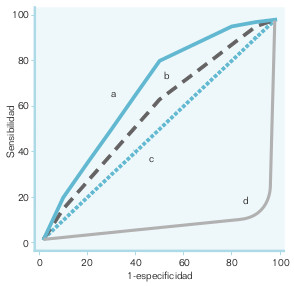
La peor de todas las representadas en la figura 15-3 es (c), ya que no discrimina.
Valores predictivos
En clínica y salud pública no se piensa en forma de sensibilidad y especificidad, ya que las pruebas diagnósticas se utilizan para guiar en el diagnóstico, y tanto la sensibilidad como la especificidad parten del conocimiento certero de lo que le sucede al sujeto. La forma habitual de utilizar una prueba diagnóstica es preguntarse si el resultado positivo o negativo que da es correcto o no. Esto introduce unos nuevos parámetros dentro de la valoración de la eficacia de una prueba diagnóstica, que son los valores predictivos.
El valor predictivo de la prueba positiva (VPP) se define como la probabilidad de que el resultado positivo de una prueba corresponda a un enfermo: VPP = VP / (VP + FP).
Esta fórmula sólo es aplicable cuando los datos de la tabla 15-4 representan adecuadamente a la población en la que se va aplicar la prueba diagnóstica. Un signo patognomónico se define como aquel que indica la presencia ineludible de la enfermedad cuando está presente. En su concepto está el que el VPP es del 100% (todos enfermos cuando el signo es positivo). De ello se deriva que no hay FP y, por lo tanto, la especificidad también es del 100%. Su sensibilidad, por el contrario, puede ser muy baja. En la estimación del VPP influye también la prevalencia (P).
Para estimar el VPP que una prueba de validez conocida puede alcanzar en una población en la que se conoce la prevalencia, se aplica la siguiente ecuación derivada del teorema de Bayes:
$$VPP = \frac{P \times S}{P \times S + \left (1 - P \right ) \left (1 - E \right )}$$
El valor predictivo de la prueba negativa (VPN) se define como la probabilidad de que un resultado negativo corresponda a un sujeto sano: VPN = VN / (VN + FN). Esta ecuación sólo se puede aplicar cuando los datos reunidos en la tabla 15-4 representan debidamente a la población en la que se va a utilizar la prueba diagnóstica. Cuando no es así, se recomienda la ecuación siguiente, derivada del teorema de Bayes:
$$VPN = \frac{ \left (1 - P \right ) E}{\left (1 - P \right ) E + P \left (1 - S \right )}$$
El valor predictivo global (VPG) es la probabilidad que tiene una prueba de acertar = (VP + VN) / (VP + VN + FP + FN). No tiene mucha utilidad per se, y ha de ir acompañada del VPP y el VPN. No es un parámetro de validez interna, ya que en su cálculo también interviene la prevalencia según la ecuación del teorema de Bayes: VPG = P × S + (1 – P) E.
La importancia de los valores predictivos se ilustrará con un ejemplo. Suponga que se aplica una prueba de glucemia para detectar la diabetes (S = 0,85 y E = 0,9) en una comunidad de 10.000 habitantes, y que se le notifica que la prevalencia de la diabetes en esa colectividad es del 1%. Los que realizan este cribado tienen que ponerse de acuerdo con los endocrinólogos para confirmar los positivos que obtienen y la primera pregunta que hace un especialista ante estudios de este tipo es: ¿cuántos sujetos se van a enviar para estudio? El número de enfermos reales que hay en la población es el producto de la prevalencia por la colectividad: 10.000 × 0,01 = 100. Los VP resultan de multiplicar la sensibilidad (0,85) por los enfermos (100); los restantes enfermos son los FN. Los VN se calculan multiplicando la especificidad (0,90) por el número de no diabéticos (9.900), y los restantes son los FP. Ahora ya se puede calcular el total de resultados positivos y negativos, y estimar los distintos valores predictivos:
VPP = 85 / 1.075 = 0,079 o 7,9%
VPN = 8.910 / 8.925 = 0,998 o 99,8%
VPG = 8.995/10.000 = 0,899 o 89,9%
(Nota: compruebe que estos valores coinciden con los resultantes de aplicar las ecuaciones del teorema de Bayes, con P = 0,01, S = 0,85 y E = 0,9)
Es posible que se pensara que, habiendo sólo 100 enfermos, no se llegaría nunca a una cifra tan elevada como 1.075 positivos, que serían los que se remitirían a los endocrinólogos para su confirmación. Además, un VPP del 7,9% indica que los especialistas se aburrirán, ya que de cada 13 pacientes sospechosos de tener la enfermedad que vean uno sólo tendrá diabetes.
La misma prueba, la glucemia, se aplica ahora en otras dos colectividades de 10.000 individuos con prevalencias más elevadas (5, 30, 70, y 95%) (tabla 15-5). Se deduce que si la sensibilidad y la especificidad son constantes, cuando la prevalencia aumenta: a) aumenta el VPP; b) aumentan en valor absoluto los FN; c) disminuyen en valor absoluto los FP, y d) disminuye el VPN. Lo contrario sucede cuando la prevalencia baja.
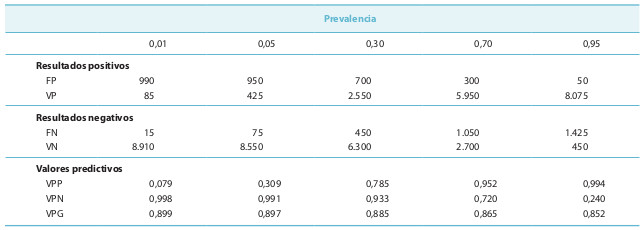
Los cambios en el VPP son muy bruscos cuando la prevalencia es inferior al 50% (que es lo habitual) y no son tan importantes sobre el VPN. Cuando la frecuencia de la enfermedad es muy elevada (ciertos ámbitos especialistas con poca diversidad de enfermedades), hay que empezar a preocuparse por los resultados negativos, ya que el VPN cae mucho. A los valores predictivos se les llama probabilidades posteriores frente a la prevalencia o probabilidad (de tener la enfermedad) anterior a la realización de la prueba diagnóstica.
La dependencia de los valores predictivos de la prevalencia tiene importantes connotaciones en clínica:
- saber que una prueba diagnóstica funciona mejor cuando la prevalencia es elevada es algo que debería tenerse en cuenta en los libros de patología;
- las pruebas no son directamente exportables de una zona a otra, a menos que la prevalencia sea similar;
- los médicos en los niveles secundario y terciario aciertan más con las mismas herramientas que utilizan los del primer nivel, con independencia de pericia, etc., ya que éstos les actúan de filtro, elevándoles la prevalencia, y
- si un médico falla con un paciente, hay que recomendarle a éste que visite otro médico y le cuente lo que le hizo el primero (el primero actúa de filtro del segundo, y así sucesivamente): un proceso raro aumenta cada vez más la posibilidad de ser diagnosticado.
El cribado suele realizarse en situaciones de baja prevalencia, de ahí la necesidad de contar con una alta sensibilidad y, además, una muy alta especificidad para evitar los FP que acarrean intervenciones innecesarias y, a veces, efectos perjudiciales (ej. la mamografía sospechosa de cáncer de mama).
Razones de verosimilitud
Las razones de verosimilitud (likelihood ratios) (RV) resumen el significado de la sensibilidad y la especificidad. Tienen un fuerte arraigo en el mundo anglosajón, ya que se basan en el concepto de odds o ventaja (el cociente de una probabilidad dividida por su complementario) y se les considera los mejores parámetros para la toma de decisiones de una prueba diagnóstica. La razón de verosimilitud positiva (RVP) relaciona a la ventaja preprueba de diagnosticar la enfermedad con la ventaja posprueba de un resultado positivo. La ventaja preprueba es la odds de prevalencia [P / (1 – P)] y la posprueba es la del VPP:
$$\frac{VPP}{1 - VPP} = \frac{P}{1 - P} \times \frac{S}{1 - E}$$
Ventaja posprueba de un resultado positivo = ventaja preprueba de enfermedad × razón de verosimilitud positiva.
Cuanto mayor sea la RVP sobre la unidad, más importante será la contribución de un resultado positivo de la prueba en el diagnóstico de la enfermedad. Una RVP = 9 indica que el resultado positivo es proporcionalmente nueve veces más frecuente en los enfermos que en los no enfermos.
Para interpretar la RVP se ofrece la escala siguiente: >10, excelente; 5-10, buena; 2-5, regular, y 1-2, pobre. Una RVP <1 indica que la sensibilidad y la especificidad son <0,5, lo cual sugiere que los criterios diagnósticos (+/–) deberían intercambiarse.
De manera clásica, la razón de verosimilitud negativa (RVN) se define como el cociente del complementario de la sensibilidad entre la especificidad. Según este concepto, y aplicando el teorema de Bayes, la RVN es la conexión entre la ventaja preprueba de enfermedad y el inverso de la ventaja posprueba del resultado negativo:
$$\frac{1 - VPN}{VPN} = \frac{P}{1 - P} \times \frac{1 - S}{E}$$
Inverso de la ventaja posprueba de un resultado negativo = ventaja preprueba de enfermedad × razón de verosimilitud negativa.
Definida así, la RVN valora la contribución que realiza un resultado negativo en la no confirmación de la enfermedad y resulta difícil de entender. Se mueve en una escala inversa a la de la RVP, y es tanto más importante cuanto más se aproxima a 0; por ello, no puede compararse directamente con la RVP. Las desventajas anteriores se eliminan si la RVN se define al revés, E / (1 – S). Entonces establece la relación entre la ventaja preprueba de no enfermedad y la ventaja posprueba del resultado negativo, que es más fácil de entender: valora la contribución de la prueba en la confirmación de que no se tiene la enfermedad. Se mueve en la misma escala que la RVP, lo que permite la comparación directa con la RVN.
Diseños que deben utilizarse para valorar una prueba diagnóstica
El aspecto central en la selección de la población es que represente a los pacientes o a la población en la que se aplicará la prueba. Esto debe ser así por la influencia que la prevalencia de la enfermedad tiene tanto en la concordancia como en la validez. Por ejemplo, suponga que quiere valorar la reproducibilidad intraobservador en la detección de soplos cardíacos en un médico. No da igual hacerlo con una muestra de reclutas que con una muestra de pacientes hospitalizados en la sala de cardiología. La elección de la población a estudio es tan clave en los estudios de validez diagnóstica que esta investigación se clasifica por fases de acuerdo con esta elección, desde los estudios en fase I que comparan personas con la enfermedad y personas sin la enfermedad hasta los estudios en fase IV en la que se selecciona a población en la que efectivamente se aplicará la prueba. En las fases I y II se comparan sucesivamente personas que aumentan el reto discriminatorio de la prueba (diferente comorbilidad, ej. en la fase II) o personas que por sus características especiales (ej. enfermedades autoinmunes) podrían dar lugar a una mayor frecuencia de resultados FPo FN.
Si la población sobre la que se trabaja cambia con el tiempo (la enfermedad evoluciona y hace más fácil el diagnóstico, aumenta así la reproducibilidad y la sensibilidad), las observaciones deben hacerse lo más próximas posible en el tiempo, para que la comparabilidad sea máxima. Si hay estabilidad en el tiempo, las distintas pruebas pueden aplicarse en distintos momentos del tiempo, si no cambian los criterios de valoración.
Una de las condiciones que siempre hay que exigir es que haya independencia entre las observaciones, que los resultados de una valoración no influyan en la otra. Si la valoración diagnóstica la hace el hombre, es conveniente que esté enmascarado frente a cualquier característica que pueda facilitar la toma de decisiones y estandarizar el proceso lo máximo posible. Hay que tener cuidado con el efecto Hawthorne. Si el sujeto sabe que está siendo objeto de una investigación, su capacidad de ejecución probablemente no será la media y será mucho más cuidadoso. Esto pudo justificar en parte los resultados que se observaron en un estudio en el que se valoró la evaluación de la variabilidad del diagnóstico rápido de infección por Chlamydia trachomatis mediante inmunofluorescencia directa por dos técnicos. En una primera etapa, los sujetos desconocían que estaban siendo investigados. Para analizar las discordancias, se habló con los técnicos y se volvió a realizar una segunda tanda. Hubo una mejora significativa en la concordancia entre la primera y la segunda evaluación en ambos técnicos.
Existen varias opciones de diseño, con el recordatorio de que una prueba valora al sujeto en un punto concreto dentro de la historia natural de la enfermedad. Si la prueba no está aceptada y se introduce por el investigador, se está ante un estudio experimental, pero donde la existencia de seguimiento tiene generalmente carácter de excepción. Los principales diseños de observación que se aplican son los siguientes:
Estudio de corte
Es el único que se utiliza en la valoración de la reproducibilidad y el segundo más usado en el estudio de la validez (y el que causa menos problemas). La prueba se aplica a una muestra representativa (una serie consecutiva) de los sujetos en los que luego se utilizará, y todos los resultados, positivos y negativos, se confirman mediante la prueba de referencia. Estos estudios generalmente se hacen sobre una serie de pacientes dentro del diagnóstico diferencial de la enfermedad que debe diagnosticarse. Todos los parámetros comentados (sensibilidad, especificidad, valores predictivos) se estiman sin problemas, ya que se obtiene una estimación de la prevalencia de la condición en estudio. Son aspectos centrales indicar qué cometido se pretende para la prueba (diagnóstico diferencial, cribado, confirmación, diagnóstica, etc) y seleccionar una población de acuerdo con ese cometido y que represente a los pacientes o a la población (si es una prueba de cribado) en la que con posterioridad se aplicará la prueba.
Estudio de casos y controles
Es el diseño más usado en el estudio de la validez, y también el que da más problemas. Se selecciona un grupo de sujetos que tienen la enfermedad diana y otro que no la tiene, según los resultados de la prueba de referencia. Dependiendo de la fase de investigación, se seleccionan casos y controles más o menos comparables a la población clínica real en la que se pretende usar la prueba.
En la fase final (IV), los casos deben representar adecuadamente el espectro de la enfermedad y no ceñirse exclusivamente a los más graves, como se hace con frecuencia. Los controles deben representar el conjunto de diagnósticos diferenciales de la enfermedad problema. En los enfermos se estima la sensibilidad y en los no enfermos, la especificidad.
Si los enfermos no mantienen la proporción (prevalencia) debida con respecto a los no enfermos, no se pueden estimar los valores predictivos (su cálculo es un error muy frecuente). En esta situación hay que obtener la prevalencia de otras fuentes o realizar un análisis de sensibilidad, variando la prevalencia dentro de un rango razonable. Si el proceso se lleva a cabo prospectivamente, no suele haber otros problemas de sesgo. No sucede así cuando la valoración se hace de manera retrospectiva; en este caso hay que reconstruir la secuencia de pruebas diagnósticas y si se realizaron a todos los individuos por igual.
Estudio de cohortes
Se usan con menos frecuencia. La prueba se aplica a una muestra representativa de sujetos de la población de referencia. Hay dos cohortes: los que dan un resultado positivo y los que lo dan negativo. El seguimiento confirma el resultado negativo, porque razones éticas o de índole económica impiden la aplicación del criterio de verdad a estos sujetos. Por ejemplo, suponga que se quiere evaluar la detección de sangre oculta en heces en el diagnóstico precoz del cáncer de colon. Los que dan un resultado positivo pueden evaluarse mediante colonoscopia y posterior biopsia. Esta valoración no está exenta de complicaciones, por lo que su uso está difícilmente justificado en los que dan un resultado negativo. El seguimiento se puede utilizar para verificar el resultado negativo, si al cabo de un cierto tiempo en estos sujetos no se diagnostica el cáncer, se considerará que el resultado fue un VN; si, por el contrario, en el intervalo aparece un cáncer de colon, éste tenía que estar presente cuando se les realizó la determinación de sangre oculta en heces, y es, por lo tanto, un FN. El intervalo de tiempo se define por el propio investigador y es crucial; en el ejemplo expuesto fue de 2 años.
Estudios de impacto diagnóstico-terapéutico y de resultados en salud
Más allá de determinar la reproducibilidad y la validez de las pruebas, cada vez es más habitual que se investigue si la información proporcionada por una prueba modifica el diagnóstico previo del clínico y su intención terapéutica. Para ello, se pide a los médicos que indiquen cuál es su juicio diagnóstico y qué tratamiento indicarían antes de realizar la prueba diagnóstica. Después, y a la luz de los resultados, deben indicar si cambian sus juicios previos. También comienza a ser corriente comprobar que para determinar si la introducción de una prueba diagnóstica mejora finalmente la salud de los pacientes se introduzca mediante estudio experimental con asignación aleatoria (ej. el uso de la ecografía en el diagnóstico de la apendicitis). Se trata de comprobar si ciertas tecnologías que pueden mejorar el detalle diagnóstico modifican también los resultados finales.
Sesgos en la valoración de pruebas diagnósticas
Sesgos de selección
Asumir que los valores de una prueba diagnóstica son constantes en diferentes subpoblaciones de pacientes puede no ser cierto. Se trata de un aserto que con frecuencia se realiza en la toma de decisiones en la clínica. Por ejemplo, en el diagnóstico de la enfermedad coronaria se ha comprobado que la prueba de ejercicio no da los mismos valores de sensibilidad y especificidad en distintos subgrupos de pacientes; influye el sexo (mejor sensibilidad y peor especificidad en los hombres), la presión arterial sistólica basal y durante el ejercicio, etc. Esto pone de manifiesto describir con detalle el ámbito en el que se ha hecho el estudio, los criterios de selección y exclusión, así como la descripción detallada de la muestra a estudio y la presentación de un análisis por subgrupos clínicamente relevantes (edad, sexo, comorbilidad, etc). De esta forma, el lector puede determinar si los pacientes estudiados son comparables al paciente al que desea aplicar la prueba, y también comprobar si es una prueba que modifica su validez según ciertas variables. El aspecto que más influye en la validez es la gravedad de la enfermedad: la sensibilidad mejora cuanto más avanzada es ésta.
En un diseño de casos y controles, el error más popular que se comete es la sobreinterpretación de los estudios en fases preliminares, cuando se comparan sujetos claramente enfermos (en los que no cabe la menor duda diagnóstica) con sujetos sin ninguna o escasa enfermedad. La validez estimada suele ser alta, pero deberá comprobarse en poblaciones clínicas reales. Esto justifica que inicialmente muchas pruebas parezcan prometedoras y luego decaiga el entusiasmo al aplicarse dentro del contexto real, con pacientes limítrofes. Ésta es la historia del antígeno carcinoembrionario en el cáncer de colon. En una primera etapa se compararon estadios III de Dukes (cáncer invasivo) con donantes sanguíneos. Al aplicarse en estadios menos avanzados y en pacientes con otra patología digestiva perdió capacidad discriminativa, y hoy simplemente ha quedado como un marcador pronóstico.
Si la prueba diagnóstica se analiza retrospectivamente, hay que garantizar que no influya en la realización ulterior del criterio de referencia, o sesgo de verificación (work-up bias): cuando a los pacientes que dan positivo en la prueba se les practica con más frecuencia la prueba de referencia que a los negativos; por ejemplo, los pacientes con una prueba de ejercicio positiva se les realiza con más frecuencia una angiografía coronaria (no se justifica una prueba invasiva sin alguna evidencia de lo que posiblemente se encontrará). En presencia del sesgo de verificación, la consecuencia suele ser la misma, la muestra pierde representatividad, ya que el número de resultados positivos (verdaderos y falsos) aumenta en relación con los negativos (la sensibilidad aumenta, mientras que la especificidad disminuye) y la prevalencia aumenta en todos los casos. Esto subraya la precaución que hay que tener con los datos retrospectivos en los que se sospecha la existencia de un sesgo de verificación.
Otro error común que se comete en la valoración de pruebas diagnósticas es la exclusión de los casos dudosos; los resultados de las pruebas diagnósticas no son siempre positivos y negativos claros. Los dudosos con frecuencia no figuran en la metodología de un estudio, por lo que no se sabe si se han producido y cómo se han procesado. La exclusión de estos casos tiene como consecuencia inmediata aumentar la sensibilidad y la especificidad.
Sesgo de información
En la valoración de una prueba diagnóstica hay que garantizar que su lectura se haga de manera independiente de la del criterio de referencia. Con ello se evita el sesgo de revisión. Una radiografía de tórax no tiene por qué verse igual si el clínico conoce la existencia de un Mantoux de 20 mm de diámetro, y una lesión dudosa puede ser adscrita más fácilmente a una probable tuberculosis basándose en ese conocimiento adicional. De ahí la ignorancia que debe existir del valor de la prueba de referencia a la hora de evaluar la prueba diagnóstica. En los estudios de concordancia es obvio que los observadores no deben comunicarse entre sí pues se incrementaría engañosamente el acuerdo.
Que la experiencia puede influir en el diagnóstico es algo que se reconoce de manera clásica. La experiencia en el campo diagnóstico se podría definir en parte como la integración subjetiva de la prevalencia de la enfermedad y las características del entorno clínico de trabajo dentro de la experiencia clínica. Si se espera una frecuencia elevada de la enfermedad, hay una tendencia a aumentar la sensibilidad y a disminuir la especificidad, sobre todo si la patología es grave y no debe pasar desapercibida.
Los individuos que tienen mayor probabilidad de ser erróneamente clasificados son los que tienen un valor real del parámetro diagnóstico próximo al punto de corte (cuanto más alejado, menor es la probabilidad de error). Los valores del parámetro diagnóstico dependen del espectro de enfermedad que existe en una colectividad, y éste es un determinante de la prevalencia de enfermedad diagnosticada y, además, influye en la mala clasificación de los individuos si, como se ha mencionado, abundan los casos con valores del parámetro diagnóstico en la frontera del punto de corte.
Esto establece una relación entre la prevalencia de enfermedad y los parámetros de validez interna de una prueba diagnóstica: sensibilidad, especificidad y RV. Lo habitual es que un aumento de la frecuencia de la enfermedad incremente Estudio de las pruebas diagnósticas la sensibilidad y descienda la especificidad. Lo anterior supone que la clásica dependencia de los valores predictivos con la prevalencia se mitiga en parte. Las RV también se ven influidas por esto: ambas (definiendo la RVN como el inverso de ésta) se asocian negativamente con el error de medición.
Errores aleatorios
Aún puede observarse que algunos investigadores usan pruebas de contraste de hipótesis comparando sensibilidad y especificidad para determinar el error aleatorio de un estudio de validez, cuando lo apropiado es presentar los intervalos de confianza de los índices estimados. Pero en esta área el problema emergente y que se observa con más frecuencia es el error denominado overfitting, al que son específicamente proclives los estudios diagnósticos basados en la genómica. Este error puede ocurrir cuando un gran número de variables predictoras (genes o proteínas) es utilizado para diferenciar la enfermedad en una muestra pequeña de individuos. El problema reside en que aunque aparentemente se muestre una correcta clasificación de los pacientes, este perfil puede no reproducirse en una muestra diferente. Hay distintos métodos para su evaluación o atenuación; sin embargo, la forma más efectiva consiste en validar la prueba en una muestra diferente a aquella que ha sido utilizada para la determinación inicial del perfil genético o proteico. La regla principal radica en seleccionar una muestra de pacientes suficientemente grande y representativa de aquellos en los que se va a aplicar la prueba diagnóstica en la práctica.
Directrices para interpretar un artículo de pruebas diagnósticas
Cuando se analiza un artículo sobre pruebas diagnósticas, hay que plantearse su evaluación dentro de tres ejes básicos: la validez de los resultados, su forma de presentación y la aplicación de éstos.
Validez de los resultados
Las preguntas fundamentales que hay que plantearse ante la lectura del «Material y métodos» de un artículo de este tipo son:
- ¿Se hizo una comparación independiente y ciega con un criterio de referencia? ¿Intenta evitar un sesgo de mala clasificación? Es más fácil que este criterio se cumpla en los estudios prospectivos.
- ¿La muestra incluye un espectro apropiado de pacientes en los que se aplicará la prueba diagnóstica?
- ¿Los resultados de la prueba en evaluación influyeron en la decisión de realizar el criterio de referencia?
- ¿Se describieron los métodos de la prueba con suficiente detalle como para permitir su replicación?
Exposición de los resultados
Debe haber datos sobre la probabilidad preprueba, y si el diseño no permite su cálculo, hay que indicarlo. En la bibliografía médica anglosajona se insiste sobre la prioridad que tiene la presentación de las RV.
Aplicabilidad de los resultados
La aplicabilidad de los resultados depende de la validez externa de la investigación.
En la valoración de ésta intervienen criterios subjetivos.
Como guía se sugiere que para valorar la validez externa se analice la reproducibilidad de la técnica en otro medio y el espectro de enfermos en los que se ha aplicado.
Con independencia de lo anterior, hay que valorar la utilidad de los resultados: si la prueba cambia la decisión sobre los pacientes. Una forma de aproximarse a esto es mediante el cálculo de la proporción de los sujetos que tienen valores muy altos de las RV, que son los individuos en los que se alcanza una razonable exactitud diagnóstica. La utilidad de los resultados está también unida a un aspecto que no debe olvidarse nunca y es que una prueba debe aplicarse para mejorar el estado de los pacientes, es decir, va ligada a una intervención preventiva o terapéutica.
En la evaluación de artículos también se recomienda la aplicación del protocolo STARD (STAndards for Reporting Diagnostic Accuracy), que se puede conseguir gratuitamente en la página web http://www.consort-statement.org/.