Medición de los Fenómenos de Salud y Enfermedad

Introducción

Todo estudio epidemiológico puede considerarse como un ejercicio de medición. De hecho, una de las tareas centrales de la investigación epidemiológica es cuantificar la frecuencia de la enfermedad o de otros problemas de salud en una determinada población.

La medición de la frecuencia absoluta de la enfermedad, así como de sus variaciones geográficas y temporales, constituyen elementos necesarios para la investigación etiológica y para la instauración de las medidas de prevención y control. Esta medición no sólo tiene interés para la investigación clínica y epidemiológica, sino también para la propia práctica clínica, en la medida en que permite orientar el diagnóstico y el tratamiento.

Las medidas epidemiológicas se basan en las cuatro medidas matemáticas habituales para determinar la frecuencia de cualquier suceso. Éstas son:

Número. Número de personas que presentan una enfermedad. Por ejemplo, decimos que se han detectado 60 casos de hepatitis C.

Proporción. Cociente de dos frecuencias absolutas en el que el numerador está incluido en el denominador. Por ejemplo, la proporción de ancianos en la Comunidad Valenciana se obtendrá mediante el cociente del número de ancianos (781.186) con respecto al total de la población (4.806.908) que incluye a los ancianos. 781.186 / 4.806.908 = 0,16, o equivalentemente, 16%. Las proporciones con frecuencia se expresan en porcentajes; para ello, se multiplica el resultado del cociente por 100. Una proporción puede considerarse como la estimación de una probabilidad cuando se calcula en una muestra representativa de una determinada población. Como ya señalaremos cuando se traten las medidas de incidencia y prevalencia, las proporciones hacen referencia a un período de tiempo definido a conveniencia por nosotros.

Razón. Cociente de dos cantidades en el que el numerador no está incluido en el denominador. Por ejemplo, el índice de masa corporal (IMC) es una razón que se define como la razón entre el peso expresado en kilogramos y el cuadrado de la talla expresada en metros.

Tasa. Razón de cambio entre dos magnitudes. A diferencia de las proporciones y razones, la tasa incluye el tiempo que tarda en aparecer el suceso en su algoritmo de cálculo, lo que permite medir la velocidad de su aparición. Existen cuatro tipos de tasas: instantáneas, promedio, absolutas y relativas.

La velocidad nos brinda un buen ejemplo para diferenciar entre tasas instantáneas y tasas promedio. Si estamos circulando en un vehículo y en un momento determinado miramos el cuentakilómetros, podrá marcar, por ejemplo, 100. En ese caso decimos que la velocidad es de 100 km/h.

Para afirmarlo, no hace falta que estemos toda una hora conduciendo, ni que recorramos 100 km. Se trata de una tasa instantánea que implica que, si continuáramos conduciendo durante una hora a esa velocidad constante, recorreríamos 100 km. Alternativamente, si realizamos un viaje de 100 km, habrá momentos en los que circularemos a 80 km/h (velocidad instantánea) y momentos en que circularemos a 120 km/h (velocidad instantánea). Si realizamos el trayecto justo en 1 h, podemos decir que la velocidad media ha sido de 100 km/h. Ésta es una tasa promedio, que es la que utilizamos habitualmente.

Una tasa absoluta es, nuevamente, la velocidad, que es el cociente entre la distancia recorrida (en kilómetros) y el tiempo transcurrido (en horas). Otra tasa absoluta es el número de casos que ocurren por unidad de tiempo. Una tasa relativa es el cociente entre la variación relativa de una variable respecto a la variación de otra variable. En epidemiología estamos interesados en tasas relativas.

Para diferenciar entre tasa absoluta y tasa relativa, supongamos que seguimos a un grupo de 5.000 personas a lo largo de 10 años para determinar el número de casos de una enfermedad que aparecen en ese grupo. Inicialmente, ninguno de los 5.000 individuos presenta la enfermedad, pero a lo largo de los 10 años aparecen 250 casos.

Definimos la tasa (promedio) absoluta (TPA) como la variación de una variable (Y) con respecto a la variación de otra variable (X). Si la variación en Y representa el cambio en el número de casos —es decir, el cambio en el estado de sano a enfermo— y la variación en X representa el cambio en el número de años transcurridos, entonces:

$$TPA = \frac{Y_{0} - Y_{1}}{X_{1} - X_{0}} = \frac{5000 - 4750}{10} = 25 c/a$$

Imaginemos ahora que decidimos ampliar el estudio, y en vez de realizarlo con 5.000 individuos lo hacemos con 10.000. Supongamos también que la proporción de casos que aparecen a lo largo del estudio (5%) no se modifica. Por lo tanto, a lo largo de los 10 años del estudio ampliado aparecerán 500 casos. Si la proporción de casos que surgen y el tiempo de seguimiento no se han modificado, cabría esperar que la tasa no se modificara tampoco. Sin embargo:

$$TPA = \frac{Y_{0} - Y_{1}}{X_{1} - X_{0}} = \frac{10000 - 9500}{10} = 50 c/a$$

Por consiguiente, si utilizamos una tasa absoluta, la velocidad de aparición de casos depende del número de individuos que participan en el seguimiento. Por ello, necesitamos tener en cuenta el promedio de personas sometidas a seguimiento. Si definimos la tasa (promedio) relativa (TPR) como la variación relativa (relativa al promedio de personas en seguimiento) de una variable (Y) respecto a la variación de otra variable (X), y definiendo Yp como el promedio de personas en seguimiento (Y₀ + Y₁ )/2, entonces:

$$TPR = \frac{\frac{Y_{0} - Y_{1}}{Yp}}{X_{1} - X_{0}}$$

Aplicado a los datos de la primera situación, tendremos:

$$= \frac{\frac{5000 - 4750}{4875}}{10} = \frac{5000 - 4750}{4875 \times 10} = 0,005 c/a$$

Del mismo modo, utilizando el estudio ampliado obtendremos ahora el mismo resultado para la tasa promedio relativa:

$$= \frac{\frac{10000 - 9500}{9750}}{10} = \frac{10000 - 9500}{9750 \times 10} = 0,005 c/a$$

Es decir, el denominador de la tasa son personas/tiempo, puesto que está formado por el promedio de individuos seguidos a lo largo del período y por el tiempo en años de seguimiento. Las tasas promedio relativas son las que se utilizan habitualmente en epidemiología. A partir de lo expuesto, resulta evidente que un período de seguimiento de 100 personas/año puede conseguirse siguiendo a 100 personas durante 1 año, a 50 personas durante 2 años o a 200 personas durante 6 meses. Dado que una tasa es una medida de cambio, su cálculo implica necesariamente el seguimiento de los sujetos para valorar el cambio a lo largo del período.

Incidencia y prevalencia

Existen dos formas de medir un fenómeno de enfermedad: o bien contamos los individuos que cambian de estar sanos a estar enfermos, o bien contamos los individuos que en un momento determinado están enfermos. En estas dos formas se basan las medidas de frecuencia de los sucesos: la incidencia y la prevalencia, respectivamente.

Incidencia

La incidencia de una enfermedad es el número de casos nuevos que surgen en una población a lo largo de un determinado período de tiempo.

Las dos medidas habituales de incidencia, que reflejan conceptos distintos, son la incidencia acumulada y la tasa de incidencia. La incidencia acumulada valora el riesgo de que se produzca un suceso. La tasa de incidencia valora la velocidad de aparición de los nuevos casos con respecto al tamaño de la población.

Incidencia acumulada

La incidencia acumulada (IA), también conocida como proporción de incidencia o riesgo, es la proporción de personas de una población que desarrollarán la enfermedad a lo largo de un período de tiempo determinado. Si definimos el riesgo como la probabilidad de que un individuo contraiga una enfermedad a lo largo de un período de tiempo determinado, la IA no mide este riesgo individual sino que mide el riesgo promedio de desarrollar la enfermedad.

Imaginemos un estudio en el que un grupo de 6 individuos es seguido a lo largo del tiempo. Tanto el inicio como la duración de los períodos de seguimiento son variables. Cuando el seguimiento de todos y cada uno de los miembros de la población es completo, el cálculo de la IA se basa simplemente en el número de sucesos acaecidos a lo largo del período de seguimiento dividido por la población inicialmente sana:

$$IA = \frac{nº\ casos\ nuevos\ en\ periodo}{población\ libre\ de\ enfermedad\ al\ inicio}$$

Sin embargo, en este ejemplo no podríamos calcular la incidencia acumulada a 4 años, puesto que no se les sigue a todos durante ese tiempo.

La IA, por ser una proporción, carece de dimensión y sus valores oscilan entre 0 Y₁. Sin embargo, en este caso, el valor de la IA se incrementa con la duración del período de estudio, por lo que debe especificarse. No es lo mismo comparar el número de casos acumulados a lo largo de 1 año con los casos acumulados a lo largo de 3 años.

Si deseamos conocer cuál es el riesgo promedio que presenta un determinado individuo de esa población de contraer la enfermedad durante un período de 2 años tras iniciarse el seguimiento, debemos observar que los 6 individuos fueron seguidos como mínimo durante 2 años completos, y que dos de ellos (sujetos 1 y 6) desarrollan la enfermedad durante los primeros 2 años. La IA (riesgo promedio) será, por lo tanto: 2 / 6 = 0,33 (es decir, 33%).

Como indicamos anteriormente, la IA es una proporción, por lo que puede calcularse su intervalo de confianza (IC) utilizando los métodos adecuados para las proporciones:

$$IC \left (95\% \right ) de IA = IA \pm 1,96 \sqrt{\frac{IA \times \left (1 - IA \right )}{n}}$$

Sin embargo, en la mayor parte de los estudios epidemiológicos el seguimiento es incompleto para la mayoría de individuos, ya que éstos desaparecen del estudio o fallecen por causas no relacionadas con el objetivo del estudio, o se incorporan tarde. En estas situaciones se dice que las observaciones están censuradas. Las técnicas habituales para el cálculo de la IA en presencia de observaciones censuradas son las tablas de vida (método actuarial) y las curvas de Kaplan-Meier.

Tasa de incidencia

La tasa de incidencia constituye la segunda manera de medir la incidencia. Puede calcularse a partir de datos individualizados o de datos agregados.

Tasa de incidencia calculada a partir de datos individualizados

La necesidad de esta medida viene determinada por la imposibilidad de la IA para captar ciertos fenómenos relacionados con el tiempo. Imaginemos que realizamos un hipotético ensayo clínico con dos grupos de 4 personas cada uno, para comparar la proporción de recidivas que se producen entre los individuos operados según dos técnicas quirúrgicas distintas (A y B) para el tratamiento de una determinada enfermedad.

Supongamos que al cabo de 10 años, 3 de cada 4 pacientes han sufrido recidivas tanto con la técnica A como con la B. Por lo tanto, la IA o riesgo promedio de recidiva es de 0,75 a los 10 años. Sin embargo, esta medida no tiene en cuenta la velocidad de aparición de las recidivas, que es claramente superior con la técnica A. Para considerar el tiempo que tardan en producirse, es necesario utilizar una medida que incorpore el tiempo, y ésta es la tasa de incidencia.

Para el cálculo de una tasa de incidencia basada en datos individualizados, el numerador es el mismo que el de la IA: casos nuevos surgidos a lo largo de un período de tiempo determinado. Pero el denominador tiene en cuenta los períodos variables de seguimiento:

$$Tasa d incidencia = \frac{ncnp}{sprsp}$$

donde ncnp es “nº de casos nuevos a lo largo de un período determinato” y sprsp es “suma de los períodos de tiempo en riesgo de cada uno de los sujetos a lo largo del período de tiempo especificado (personas/tiempo)”.

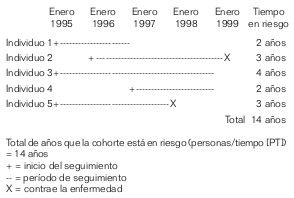
Para exponer el cálculo de las personas/tiempo del denominador de la tasa, imaginemos que realizamos un estudio (muy simplificado) con 5 personas. Este estudio comienza en enero de 1995 y finaliza en enero de 1999.

No todas las personas inician el estudio en 1995. De hecho, el individuo 2 se incorpora 1 año más tarde y el individuo 4 lo hace 2 años más tarde. En consecuencia, el número de años de seguimiento en el estudio no es similar para cada uno de los 5 participantes. Ante esta situación, una posible opción es calcular el riesgo de contraer la enfermedad a los 2 años de incorporarse al estudio, ya que todos los participantes han sido seguidos durante un mínimo de 2 años. Pero este cálculo desperdiciaría información ya que podemos afirmar que los individuos 2 y 5 están 3 años en riesgo antes de contraer la enfermedad, y el individuo 3 no contrae la enfermedad tras 4 años de seguimiento. Por consiguiente, en este contexto, la tasa de incidencia utiliza toda la información disponible.

A partir de este ejemplo podemos inferir que, cuando conocemos los períodos variables de seguimiento de cada uno de los participantes, podemos calcular tasas de incidencia basadas en datos individualizados. Así, en el ejemplo de la figura 8-4, el individuo 1 contribuye 2 años de seguimiento, el individuo 3 contribuye 4 años, etc., de tal modo que la cohorte de 5 personas contribuye con un total de 14 personas/año de seguimiento. Si observamos que a lo largo de los 4 años se han producido 2 casos, podemos calcular la tasa de incidencia:

$$TI = \frac{nº\ casos\ nuevos}{PT}$$ $$= \frac{2}{14} = 0,14 casos\ por\ persona/año\ seguimiento$$ $$= 1,4 casos\ por\ persona/decenio$$ $$= 0,012 casos\ por\ persona/mes$$

Como podemos observar, el valor numérico de una tasa carece de interpretación a menos que utilicemos las unidades temporales. Es decir, en el ejemplo anterior, si no cuantificamos el tiempo (año, decenio, 6 meses), la misma tasa puede dar valores de 0,14, 1,4 o 0,012, según las unidades utilizadas. La elección de la unidad depende del investigador, pero generalmente se elige de acuerdo con la frecuencia del suceso que se estudia. Para sucesos relativamente infrecuentes, como es el caso de la mayoría de enfermedades crónicas, se utilizan personas/año.

Vimos anteriormente cómo un período de seguimiento de 100 personas/año puede conseguirse siguiendo a 100 personas durante 1 año, a 50 personas durante 2 años o a 200 personas durante 6 meses. El cálculo de las tasas de incidencia basadas en personas/año asume implícitamente que el riesgo de que se produzca el suceso se mantiene aproximadamente constante para el período. Es decir, si en un período de seguimiento de 2 años el riesgo se concentra casi exclusivamente en los primeros 6 meses, no podríamos asumir que la estimación de incidencia basada en 50 personas/2 años fuera equivalente a la de 200 personas/6 meses.

Asimismo, la tasa de incidencia carece de interpretación individual, debido a que la tasa instantánea para cada individuo no puede calcularse directamente. Es por ello que se utiliza como aproximación la incidencia promedio en una población.

El rango de la tasa de incidencia se extiende desde cero hasta infinito, ya que tiene el rango matemático de la razón entre dos cantidades positivas. Si consideramos un estudio de 100 personas, y las 100 contraen la enfermedad, es cierto que como máximo el 100% puede contraer la enfermedad, lo que indicaría que el valor debería extenderse entre 0 y 1. Pero la tasa no es una proporción. Por eso, en 100 personas no pueden producirse más de 100 casos, pero esos 100 casos pueden aparecer en 10.000 personas/años, en 1.000 personas/años, etc. Por ello, las tasas de incidencia no pueden interpretarse como probabilidad.

La tasa de incidencia se mide en unidades inversas del tiempo. Por ello, en determinadas circunstancias la tasa permite calcular el tiempo que tardan en producirse los casos. Si interpretamos la tasa de incidencia como la inversa del tiempo promedio que transcurre hasta la aparición de un caso, una tasa de 0,14/persona/año equivaldría a que en una población de 100 habitantes, como promedio, surja un caso cada 26 días. Esto es cierto únicamente si la población se encuentra en situación estacionaria y si se asume que no existen datos censurados por muerte por otra causa o emigración. Del mismo modo, una tasa de mortalidad de 0,05 casos/persona/año equivale a que el tiempo promedio hasta que se produzcan los fallecimientos es de 20 años.

Puesto que en el cálculo de una tasa el numerador es generalmente pequeño comparado con el denominador, ya que los sucesos son relativamente infrecuentes, podemos asumir que el número de sucesos sigue una distribución de Poisson y los procedimientos para el cálculo de la variancia y el error estándar se basan en esta suposición. Aunque el modelo básico de probabilidad de la tasa de incidencia es la distribución de Poisson, el cálculo del IC para una tasa de incidencia (TI) puede realizarse mediante una aproximación por la distribución normal.

$$IC \left (95\% \right ) de TI = TI \pm 1,96 \sqrt{\frac{TI}{Personas - Tiempo}}$$

Una forma más exacta para el cálculo del IC de una tasa de incidencia se basa en la tabla de valores limitantes de una variable que sigue la distribución de Poisson (esta tabla puede encontrarse en textos de estadística). Así, según el número de sucesos en que se basa la estimación de la incidencia, la tabla facilita los valores del factor del intervalo de confianza inferior y del intervalo superior. Por ejemplo, si el número de casos en que se basa la estimación es de 10, los valores de los factores de los intervalos de confianza (95%) inferior y superior que aparecen en la tabla son 0,480 y 1,84, respectivamente. Para calcular el IC, se procede de la siguiente manera: en primer lugar, se calcula el IC para el número de casos, para lo cual se multiplica dicho número de casos por los factores de los intervalos inferior y superior; así, el intervalo inferior equivale a 10 × 0,480 = 4,8, y el superior, a 10 × 1,84 = 18,4. Posteriormente, estos valores se ponen en relación con el número de personas/tiempo del denominador. Por ejemplo, si en un determinado estudio se observan 10 casos entre 300 personas/día de seguimiento, la tasa de incidencia es de 10 / 300 = 0,033 persona/día o 33/1.000 personas/día. Hemos calculado el intervalo inferior como 4,8 y el superior, como 18,4. Ahora, 4,8 / 300 = 0,016 persona/día y 18,4 / 300 = 0,061 persona/día. Por lo tanto, el IC del 95% para una tasa de incidencia de 0,033 persona/día se extiende desde 0,016 hasta 0,061 persona/día.

Tasa de incidencia calculada a partir de datos agregados

El cálculo de la tasa de incidencia a partir de datos agregados se utiliza cuando se requiere el cálculo de la incidencia para un conjunto de individuos residentes en un área geográfica bien definida a lo largo de un determinado período de tiempo. En estas circunstancias no se dispone de datos individualizados de seguimiento. El cálculo de las tasas de mortalidad, a partir de las estadísticas de mortalidad, y el cálculo de la incidencia de determinadas enfermedades a partir de los datos recogidos por los diversos registros constituyen las áreas en las que se utilizan habitualmente.

La población residente en una zona geográfica no permanece estable, ya que en ella se producen emigraciones e inmigraciones que modifican la población en riesgo. En consecuencia, el denominador para el cálculo de la tasa de incidencia basada en datos agregados lo constituye el promedio de la población que ha residido en esta área a lo largo del período de interés. Si el período de tiempo considerado no es excesivamente largo, y si las inmigraciones se compensan aproximadamente con las emigraciones, podemos estimar el promedio de la población como la población existente a la mitad del período. Si el período considerado es 1 año, como suele ser habitual en el cálculo de las tasas de mortalidad (que son tasas de incidencia basadas en datos agregados), la población promedio es la residente en esta localidad a 1 de julio. De este modo, podemos calcular la tasa de incidencia basada en datos agregados como:

$$Tasa\ de\ incidencia = \frac{nº\ casos\ nuevos}{población\ promedio}$$

Por ejemplo, si en una determinada población con un censo de 5.000 habitantes a principios de año se produce un incremento de 600 habitantes a lo largo de los 2 años siguientes, como consecuencia de la diferencia entre emigración e inmigración, y si asumimos que dicho incremento se ha producido de manera homogénea a lo largo del período, la población promedio será la existente al final del primer año, que será de unos 5.300 habitantes. Esta información se obtiene a partir de los datos de población. Si en esta localidad se han producido 80 fallecimientos a lo largo de los 2 años, la tasa de mortalidad (TM) será:

$$\frac{80}{\frac{5000 + 5600}{2}} = 0,015/persona/2 años$$

Como se observa, la tasa de mortalidad no está basada en el número de habitantes, sino en una unidad de tiempo (persona/2 años). Es decir, se produjeron 80 casos nuevos (muertes) entre 5.300 personas/tiempo, en este caso entre 5.300 habitantes seguidos durante 2 años. El resultado puede expresarse del mismo modo por persona/año (que es lo habitual). Para ello, basta con dividir el número de fallecimientos por la duración del período:

$$\frac{\frac{80}{2}}{\frac{5000 + 5600}{2}} = 0,075/persona/años$$

Esta tasa de mortalidad de 0,0075 persona/año equivale a una tasa de mortalidad de 7,5/1.000 personas/año, lo que implica que entre 1.000 personas seguidas durante 1 año (o 500 seguidas durante 2 años) se producen 7,5 muertes. Del mismo modo, entre 10.600 personas seguidas durante 1 año (o 5.300 seguidas durante 2 años) se producen 80 muertes.

Relación entre las tasas de incidencia basadas en datos individuales y en datos agrupados

Cuando las pérdidas (emigración, muerte por otra causa) y los sucesos de interés (caso nuevo, muerte, etc.) se producen de manera homogénea a lo largo del período considerado, la tasa de incidencia por persona/tiempo (datos individuales) se corresponde con la tasa por población promedio (datos agregados), promediada por la correspondiente unidad de tiempo.

$$TPP = \frac{\frac{nº\ sucesos\ A}{PP\ N}}{tiempo\ t} =$$ $$\frac{A}{Nt} = TI\ persona/tiempo$$

donde TPP es “Tasa población promedio” y PP es “población promedio”.

Basándonos en los datos de 8 personas seguidas durante un máximo de 2 años podremos establecer las comparaciones pertinentes. Los individuos 2 y 5 contraen la enfermedad tras medio año, y los individuos 3 y 7, tras año y medio. Los datos censurados se producen al final del primer año, por emigración y fallecimiento, y al final del segundo año, por terminar el seguimiento. Por lo tanto, la censura y los sucesos de interés se producen regularmente a lo largo de los 2 años desde el inicio del estudio (a los 0,5, 1 1,5 y 2). El número total de personas/año con que han contribuido estos 8 individuos es de 10, y se han producido 4 casos. La población promedio a lo largo del período es de 5.

$$TPP = \frac{4}{\frac{\frac{8 + 2}{2}}{2}} = Tasa\ persona/tiempo$$

Esta correspondencia es precisamente la que permite el cálculo de medidas estandarizadas. Cuando los sucesos de interés y las pérdidas no se producen de manera uniforme, estas dos medidas de incidencia difieren.

Relación entre riesgo y tasa de incidencia

Para intervalos de tiempo cortos, podemos aproximarnos al riesgo de un suceso por medio de la expresión:

$$Riesgo = TI \times t$$

donde t es el período de tiempo especificado.

Si la tasa de incidencia es, por ejemplo, 0,4 casos por individuo y año, el riesgo de que ocurra el suceso a lo largo de una semana será 0,00109 × 7 = 0,00763 (nótese que 0,4 dividido por 365 días de un año = 0,00109).

Ahora bien, el riesgo de que ocurra un suceso a lo largo de un período más largo no equivale a TI × t. Por ejemplo, si la tasa de incidencia es de 0,4 casos por individuo y año, el riesgo de que ocurra un suceso en los próximos 5 años no es 0,4 × 5 = 2,0 ya que los riesgos son probabilidades y no pueden ser superiores a 1. Cuando el período de tiempo es largo, la relación entre riesgo y tasa es diferente. Consideremos a un individuo en un momento determinado. El riesgo de que a ese individuo le ocurra el suceso en el siguiente intervalo de tiempo depende de la longitud de ese intervalo. Si a un intervalo de tiempo muy corto lo denominamos h, al riesgo lo denominamos π y a la tasa, λ; entonces:

$$λ = \frac{π}{h}$$

En ese caso decimos que la tasa de incidencia es el riesgo por unidad de tiempo.

Si se considera ahora un intervalo de tiempo largo t, que esté formado por n períodos de tiempo muy cortos de duración h cada uno de ellos (es decir, t = n h), a un individuo puede ocurrirle el suceso de interés en cualquiera de esos períodos de tiempo muy cortos. En cualquiera de ellos, la probabilidad de que le ocurra el suceso (riesgo) es λ h. Se observa que esta probabilidad es condicional a que no haya sufrido el suceso en un intervalo anterior, o que se haya perdido (muerte por otras causas o pérdida). Del mismo modo, la probabilidad condicional de que no le ocurra el suceso durante ese intervalo de tiempo muy corto es 1 – λ h. Por consiguiente, la probabilidad de que observemos al sujeto a lo largo del intervalo de tiempo grande t sin que le ocurra el suceso es: (1 - λ h)ⁿ

Una propiedad importante del exponencial es que cuando x es un número pequeño y positivo, 1 + x ≈ exp (x) y también 1 – x ≈ exp (–x). Por ejemplo, exp (0,02) ≈ 1,02; exp (x) corresponde a la función matemática e^x. De lo anterior se deriva que: (1 - λh)ⁿ ≈ exp (–λh) = exp (–λt)

De hecho, (1 - λh)ⁿ equivale exactamente a exp (–λt) a medida que el intervalo h se hace infinitesimalmente pequeño. Por lo tanto, la probabilidad de que el sujeto no sufra el suceso es exp (–λt) y la probabilidad de que sí le ocurra el suceso es 1 – exp (–λt).

En otras palabras: Riesgo = 1 – exp(–TI x t)

Nótese que en la fórmula anterior, si la enfermedad es infrecuente (λ pequeña) o el tiempo de seguimiento es muy corto (h), entonces:

Riesgo = 1 – exp(–TI x t) ≈ TI x t

Por ejemplo, si en un estudio la tasa de incidencia obtenida es de 0,4 casos/persona/año, el riesgo de que ocurra el suceso a lo largo de los próximos 5 años será:

Riesgo = 1 – exp(–0,4 x 5) = 0,86

Es decir, una persona residente en la comunidad donde se realiza el estudio tiene, como promedio, un 86% de probabilidad de contraer la enfermedad a lo largo de los próximos 5 años.

Como indicamos anteriormente, la segunda medida de frecuencia es la prevalencia.

Prevalencia

Prevalencia es el número de casos (tanto antiguos como recientes) de una determinada enfermedad que existen en una población. Hay dos tipos de prevalencia: la prevalencia puntual y la prevalencia de período.

La prevalencia puntual es el número de casos de una determinada enfermedad que existen en una población en un momento determinado. Es decir, es la proporción de individuos de una población que están enfermos en un momento concreto. Ésta es la medida estimada en las encuestas de prevalencia o transversales como la Encuesta Nacional de Salud, y es la medida de prevalencia más utilizada. La referencia a un momento determinado suele ser un momento cronológico (ej. prevalencia de una enfermedad a 1 de julio), pero no necesariamente es siempre así. Por ejemplo, podemos estar interesados en la seroprevalencia de VIH en personas que ingresan en prisión, en el momento del ingreso. Es obvio que no todo el mundo ingresa en la misma fecha, pero es el momento conceptual (al ingreso) el que determina el momento t.

$$PP = \frac{ncem}{tpm}$$

donde PP es “prevalencia puntual”, ncem es “nº de casos existentes en momento (t)”, y tmp es “total de la población en momento (t)”.

En determinadas ocasiones resulta interesante conocer la prevalencia de una enfermedad a lo largo de un determinado intervalo de tiempo (t₀, t). Es lo que se conoce como prevalencia de período, que se define como el número de casos de una determinada enfermedad que existen en una población durante un período de tiempo determinado, como, por ejemplo, 1 año:

$$PP = \frac{ncem\ t_{0} + ncne}{pmi}$$

donde PP es “prevalencia de periodo”, ncem es “nº de casos existentes en momento t₀”, ncne es “nº de casos nuevos entre t₀ y t”, y pmi es “población a mitad del intervalo (t₀, t)”.

En caso de que se desconozca la población a la mitad del intervalo, se calcularía mediante la interpolación de la población inicial con la existente al finalizar el período de estudio. Una modalidad particular de la prevalencia de período es la llamada prevalencia acumulada a lo largo de la vida. Esta medida permite estimar la frecuencia de una enfermedad en cualquier momento a lo largo de la vida de un individuo.

La prevalencia es una proporción, por lo que sus valores oscilan entre 0 y 1. Como cualquier otra proporción, carece de dimensión; para que cobre significado, debe expresarse el tiempo de observación. La mayoría de las veces la prevalencia no se acota en un período de tiempo, sino que se acompaña simplemente de una fecha. Por ejemplo, decimos que en 1999 la prevalencia del sida en España era aproximadamente del 1/1.000.

La prevalencia calculada a partir de los datos obtenidos en un estudio por medio de una muestra es una aproximación a la verdadera prevalencia existente en la población. Debido a la variabilidad biológica, la prevalencia estimada diferirá en cierta medida de la prevalencia real. Por este motivo, resulta conveniente calcular un IC para nuestra medida de prevalencia, en el que muy probablemente se encuentre la verdadera prevalencia de la población. Como indicamos anteriormente para la incidencia acumulada, la prevalencia es una proporción, por lo que puede calcularse su IC utilizando los métodos adecuados para las proporciones:

$$IC \left (95\% \right ) de\ P = P \pm 1,96 \sqrt{\frac{P \times \left (1 - P \right )}{n}}$$

donde P es “prevalencia”.

Si utilizando una muestra de 1.000 personas representativa de una determinada población hemos estimado que la prevalencia de hipertensión arterial en esta población es del 20%, podremos calcular el IC como:

$$IC \left (95\% \right ) = 0,20 \pm 1,96 \sqrt{\frac{0,20 \times \left (1 - 0,20 \right )}{1000}}$$

$$= 0,225 intervalo\ superior\ y\ 0,176 intervalo\ inferior$$

Por lo tanto, la verdadera prevalencia de hipertensión en dicha población se encontrará generalmente entre el 17,6 y el 22,5%.

Aunque la prevalencia refleja adecuadamente la magnitud de un determinado problema de salud, por lo que es útil para la planificación y gestión de recursos, esta medida resulta de poca utilidad en los estudios etiológicos, ya que está en función no sólo de la incidencia sino también de la duración de la enfermedad. Por ello, a continuación describiremos la relación existente entre prevalencia e incidencia, como ya hicimos con las medidas de incidencia.

Relación entre prevalencia e incidencia

Supongamos que una determinada enfermedad se encuentra en situación estacionaria, lo que implica que la incidencia y el número de casos existentes en un momento determinado (A) son aproximadamente constantes. En el caso de una enfermedad incurable por la que todos fallecen, el número de casos nuevos que surgen a lo largo de un determinado período es aproximadamente igual al número de fallecimientos entre los casos. Si el tamaño de la población es N, la incidencia de la enfermedad es I y la tasa de letalidad es L, puede estimarse el número de casos nuevos multiplicando la incidencia por el número de personas susceptibles de contraer la enfermedad (N – A). A su vez, podemos estimar el número de fallecimientos multiplicando la letalidad por el número de casos prevalentes. Por lo tanto:

$$I \times \left (N - A \right ) ≈ L \times A$$

Si la población es estable, la tasa de letalidad es la inversa de la duración (D) de la enfermedad. Así:

$$I \times \left (N - A \right ) ≈ \left (\frac{1}{D} \right ) \times A$$

De este modo:

$$I \times D ≈ \frac{A}{\left (N - A \right )}$$

Dividiendo el numerador y denominador del término de la derecha por N encontramos que el producto de la incidencia por la duración de la enfermedad equivale a la odds de prevalencia (término que se desarrollará posteriormente):

$$= \frac{\frac{A}{N}}{\frac{\left (N - A \right )}{N}} = \frac{prevalencia}{\left (1 - prevalencia \right )}$$

Esto equivale a reformular la expresión como:

$$Prevalencia = I \times D \left (1 - Prevalencia \right )$$

En esta ecuación, la prevalencia hace referencia a la prevalencia puntual, y las unidades de tiempo para la incidencia y la duración son las mismas. En el caso de enfermedades en las que la muerte no es inevitable, el cálculo es el mismo, pero L se interpreta como la proporción de personas que se curan.

Como indicábamos anteriormente, las limitaciones de la prevalencia para el estudio etiológico se ponen de manifiesto cuando observamos que esta prevalencia depende no sólo de la incidencia sino también de la duración de la enfermedad.

A su vez, la diferencia entre incidencia y prevalencia puntual depende de la duración y de la propia magnitud de la prevalencia puntual. Si la prevalencia es muy baja, el término (1 – prevalencia) es prácticamente igual a 1, por lo que la expresión anterior se reduce a:

$$Prevalencia = Incidencia \times Duración$$

Si la incidencia de una enfermedad que ha permanecido estable a lo largo del tiempo es del 2% por año y la duración es de 10 años (desde que se diagnostica hasta la curación o fallecimiento), la prevalencia puntual de esta enfermedad en esa comunidad es del 20%.

Finalmente, tras describir las medidas de incidencia y prevalencia, y la relación entre ellas, presentamos otra medida de frecuencia de enfermedad utilizada en epidemiología, aunque de manera poco habitual: la odds.

ODDS

La odds es un término inglés que ha sido traducido como posibilidad, oportunidad o ventaja, pero que mantenemos como odds por considerar que estas traducciones no son conceptualmente informativas. La odds es un tipo de razón en la que el numerador representa la probabilidad de que ocurra un suceso y el denominador, la probabilidad de que no ocurra. Por lo tanto, puede interpretarse como la relación entre dos probabilidades complementarias:

$$Odds = \frac{POS}{1 - POS} = \frac{POS}{PONS}$$

donde POS es “Probabilidad de que ocurra un suceso” y PONS es “Probabilidad de que no ocurra el suceso”.

La odds puede definirse tanto para incidencia como para prevalencia, si bien ninguna de las dos medidas se utiliza habitualmente como medida de frecuencia. Por el contrario, la razón entre dos odds (odds ratio) es una medida de asociación utilizada con mucha frecuencia en epidemiología.

Como ejemplo del cálculo de una odds, supongamos que entre los 1.000 nacidos vivos de una localidad se han detectado 2 casos de espina bífida. La proporción de individuos con espina bífida es 2/1.000. Como estudiamos toda la población de nacidos vivos, podemos decir que la probabilidad de tener una espina bífida es 2/1.000 = 0,002. Del mismo modo, la probabilidad de no tener esta anomalía congénita es 998/1.000 = 0,998. Por lo tanto, la odds de tener espina bífida será:

$$\frac{\frac{2}{1000}}{\frac{998}{1000}} = 0,002$$

$$≈ \frac{2 casos}{998 no\ casos} = 0,002$$

Como medida de frecuencia, la odds puede presentarse como un simple número (0,002), que expresa intrínsecamente una razón (0,002:1), o directamente como una razón (2:998 o 1:499), lo que indica que en esta población por cada caso de espina bífida hay 499 que no la tienen.

Como señalaremos posteriormente, resulta útil convertir proporciones en odds, y viceversa. Generalmente resulta más intuitiva la proporción que la odds:

$$Odds = \frac{Proporción}{1 - Proporción}$$

$$Proporción = \frac{Odds}{1 + Odds}$$

Como hemos observado en el ejemplo anterior, en el que la probabilidad de tener espina bífida es baja, la probabilidad (0,002) es igual a la odds (0,002). Esto ocurre siempre que la frecuencia de la enfermedad es muy baja, ya que entonces el denominador de la odds es prácticamente 1, por lo que su valor coincide con el de la proporción. A medida que aumenta la frecuencia las dos medidas divergen.