Estudio del pronóstico y de las decisiones en clínica
Introducción
Este capítulo se ocupa de dos temas de relevancia clínica: el pronóstico y los procedimientos de toma de decisiones en la clínica, que se abordan secuencialmente.
Pronóstico es una predicción del curso futuro de la enfermedad desde el momento actual. Si tenemos un número suficiente de casos similares, la predicción la podríamos hacer en términos de probabilidad. Por ejemplo, tras sufrir un adulto una infección por el virus de la hepatitis B, ¿quedará como portador del virus? La probabilidad es de un 10%. Antiguamente, el pronóstico estaba sólo en función de la historia natural de la enfermedad, pero ahora se ha asociado a una probabilidad debidamente cuantificada e implica también la concurrencia de distintos factores: biológicos, sociales, cuidados de salud, etc. Así pues, el pronóstico es una apreciación de la gravedad de un enfermo y una predicción de la evolución de la enfermedad, según los posibles caminos tomados (con tratamiento o sin él, rehabilitación, etc), lo que será fundamental para la toma de decisión clínica.
Como resumen de las características que debe tener un pronóstico, citamos las de Fries y Ehrlich (modificadas):
- Es una predicción, de entidad incierta y probabilística.
- Puede expresarse de forma cuantitativa (mas útil, como se ve en la tabla 21-1, en la que se expresa en porcentaje la probabilidad de morir) o cualitativa, si lo anterior no es posible (ej. podemos decir que un enfermo tiene una probabilidad pequeña, moderada o grande de morir, etc).
- Es multidimensional. Se refiere a diversas consecuencias de la enfermedad (ej. curación, muerte, secuelas físicas o psíquicas, etc).
- Se asocia a un período de tiempo concreto (ej. probabilidad de sobrevivir a los 5 años, etc).
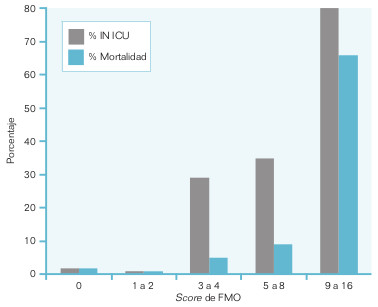
- Varía de un subgrupo de enfermedad a otro, y es necesario aplicarlo adecuadamente a cada grupo particular; así, la supervivencia de un cáncer de pulmón de células pequeñas difiere de la de otros cánceres de pulmón, o bien un cáncer en estadio II respecto de un cáncer en estadio III o IV, o la supervivencia y la probabilidad de sufrir una infección en la unidad de cuidados intensivos (UCI), varían según la puntuación del marcador de fracaso multiorgánico (fig. 21-1), etc.
- Se debe considerar separadamente el pronóstico de la enfermedad, con tratamiento y sin él.
Factores de riesgo y factores pronósticos
Los factores de riesgo y pronósticos pueden tener similitudes y estudiarse por tipos semejantes de estudios, generalmente de cohortes, pero debe distinguirse entre factores que aumentan el riesgo de enfermedad y aquellos que predicen un curso concreto de ésta, una vez que el individuo ha enfermado. Los primeros son factores de riesgo; los segundos, factores pronósticos. Así pues, un factor pronóstico es una condición que, cuando está presente en un enfermo, se asocia a un desenlace concreto de esa enfermedad. Los factores de riesgo y pronósticos forman parte de un continuo en el curso de una enfermedad, desde sus causas hasta sus consecuencias.
Veamos un ejemplo. En los accidentes de tráfico se han observado diversos hechos que actúan como factores de riesgo y otros, como factores pronósticos de muerte (incluso algunos son tanto factores de riesgo como factores pronósticos):
- Factores de riesgo de sufrir un accidente de tráfico:
- Edad (aumento desde 18-30 años).
- Sexo (hombre).
- Enfermedades neurológicas.
- Lugar (carretera 2º orden).
- Tiempo metereológico (lluvia, niebla, etc).
- Factores pronósticos de muerte por accidente de tráfico:
- Edad (aumento en >65 años).
- No llevar cinturón de seguridad.
- Enfermedades cardiovasculares.
- Lugar (carreteras segundo o tercer orden por mayor probabilidad en el retraso de la asistencia).
- Tiempo metereológico (por retraso de la asistencia).
Las principales diferencias entre estos dos tipos de factores son:
- Los factores de riesgo generales predicen eventos de probabilidad baja; así, las tasas de cualquier enfermedad se contabilizan en unas pocas unidades por 1.000, 10.000, 100.000, etc. Por ello, las relaciones entre los factores de riesgo y la enfermedad pueden escapar al conocimiento intuitivo de muchos clínicos, razón por la cual es necesario establecerlas mediante estudios apropiados, con un adecuado número de sujetos y tiempo de observación.
- Los factores pronósticos describen comparativamente pocos eventos, por lo que los clínicos experimentados pueden hacer, con su experiencia, balances aproximados de las probabilidades reales de cada uno de los desenlaces de la enfermedad.
- Hay factores de riesgo que son también factores pronósticos (el ejemplo sobre accidentes de tráfico), pero la mayoría son diferentes, máxime teniendo en cuenta que entre los factores pronósticos puede entrar toda la asistencia sanitaria al enfermo.
- También es útil distinguir los factores de riesgo de los factores pronósticos desde un punto de vista conceptual para la medicina preventiva, ya que la prevención primaria tiende a evitar o controlar los primeros, mientras que a los segundos se dedicará la prevención secundaria y terciaria.
- Por último, en los factores pronósticos hay que distinguir aquellos que actúan sólo en la historia natural de la enfermedad (que transcurre sin intervención alguna) y los que influyen en su curso clínico, en el que se interviene de alguna forma (dieta, medicamentos, cirugía, rehabilitación, etc).
El curso natural de muchas enfermedades ya no es observable, y sólo se tienen referencias de él en la bibliografía médica. No obstante, hay enfermedades nuevas en las que se tienen descripciones recientes, previas a cualquier tratamiento (ej. el sida) y también puede observarse el curso natural en un gran número de afecciones leves que se consideran problemas habituales y que pocas veces llevan a una intervención clínica (depresiones leves, anemia leve, etc). Sin embargo, cuando alguna de estas enfermedades, por leve que sea, produce dolor, gran malestar, etc, inducirá a recurrir a la atención médica, y entonces se entrará en el curso clínico de la enfermedad, que es aquella parte de la historia de la enfermedad bajo cuidado médico, con sus tratamientos y posibles desenlaces.
Al considerar sólo el curso clínico de la enfermedad, ya existe un sesgo de muestreo, pues los enfermos más graves tienen más probabilidad de haber recurrido a la atención médica. Así, por comodidad y accesibilidad, la mayoría de los estudios sobre pronóstico se realizan sobre enfermos durante su paso por el hospital, estando sujetos, como se comenta en otro capítulo, al sesgo de Berkson, que está en relación con aquellos factores que llevan a remitir al enfermo desde atención primaria hasta el hospital, etc.
Por ello, al trazar un árbol de probabilidades sobre los posibles desenlaces de la enfermedad, hay que ser muy cautos al extrapolar conclusiones y ceñirlas sólo al tipo de enfermos que estamos viendo, pues, de lo contrario, se estaría cometiendo un sesgo hacia la zona más grave del espectro de la enfermedad.
Establecimiento de un pronóstico
La descripción de un pronóstico debe incluir el rango completo de manifestaciones que se consideren importantes en los pacientes de esa enfermedad. Así, debe incluirse no sólo muerte o curación, sino también dolor, angustia, imposibilidad de autocuidados, etc, que no siempre están asociados a eventos de relevancia clínica. Por ejemplo, un enfermo no percibe bien si su tumor se redujo o no, pero sí que el dolor se controló o agudizó. Los médicos pecamos a veces de lo contrario, al valorar más la información clínica que tiene poca relevancia para la calidad de vida del enfermo, aunque sí la puede tener para el diagnóstico, etiología, etc, de la enfermedad.
Cuando se va a establecer un pronóstico de una enfermedad, se debe reunir una cohorte de enfermos en el tiempo «0». Éste puede ser el comienzo de los síntomas, el momento del diagnóstico, etc, dependiendo de la enfermedad. Si distintos investigadores comienzan el estudio en puntos distintos de la historia de la enfermedad, las observaciones tendrán poca correlación y los desenlaces serán más difíciles de interpretar en función de los factores pronósticos.
Por ejemplo, si incluimos en una «cohorte» a mujeres con cáncer de útero, pero que provengan unas del cribado de esta enfermedad, otras de un diagnóstico de sospecha por su sintomatología en un ambulatorio, y otras procedentes de ingresos hospitalarios para intervención quirúrgica del tumor, no podemos llegar a ninguna conclusión sobre los resultados, ya que todo dependerá de la frecuencia relativa de estos tres subgrupos de enfermas en nuestra muestra.
La finalidad en un pronóstico debe ser doble:
- Identificar los factores pronósticos de los enfermos, con vistas a la toma de decisiones terapéuticas.
- Evaluar los resultados de una intervención particular, buscando, en realidad, cambiar el pronóstico mismo de la enfermedad.
Se ha observado, de este modo, que los enfermos que tienen lesionada su válvula aórtica (ej. de nacimiento o tras una infección, etc), pero que se mantienen asintomáticos, tienen una supervivencia semejante a las personas sin esta lesión, por lo que la intervención precoz (antes de presentar sintomatología) no resuelve nada. Sin embargo, el horizonte cambia en aquellos enfermos con una válvula calcificada, ya que tras esto, la probabilidad de morir o requerir una intervención urgente para el recambio valvular en los 4 años siguientes es del 60-80%. En estos casos, la intervención precoz sí produce un incremento en la supervivencia y en la calidad de vida.
Para hacer un buen pronóstico, es preciso tener en cuenta los puntos que a continuación se mencionan:
- Consideraciones previas:
- El estado de los sujetos incluidos en nuestro estudio, al comienzo del seguimiento, debe ser comparable.
- El estudio debe durar el tiempo suficiente para apreciar resultados de evolución. Para lo cual nos basaremos en datos de la bibliografía científica o en nuestra experiencia. Si el tiempo es demasiado corto, las conclusiones suelen ser más optimistas que la realidad (no da tiempo a manifestar las complicaciones) o más pesimistas (no da tiempo a la recuperación en algunos casos de evolución más lenta).
- Los estudios pronósticos sobre el curso clínico deben tener en cuenta los tratamientos y, además, estos tratamientos deben ser comparables de un sujeto a otro, tanto por parte del clínico como del enfermo (cumplimiento terapéutico).
- Hay que tener en cuenta todos los posibles resultados de la enfermedad y valorar el hecho de que éstos no dependen sólo del procedimiento terapéutico, sino que muchos tienen su propia evolución, a pesar del tratamiento instituido.
- Los pronósticos son mejores cuanto más objetivas sean las consecuencias que hemos elegido para valorar. Por ejemplo, la muerte, la infección, etc, son mejores que el dolor, el bienestar, etc. Para esta última clase de consecuencias, muchas veces hay que recurrir al consenso de expertos con objeto de establecer índices o puntuaciones que nos ayuden a definir con más exactitud lo que queremos medir (ej. en pacientes con resección de estómago por cáncer gástrico, Marubini et al. [1993] obtuvieron como factores pronósticos que influían significativamente en la supervivencia a 5 años la edad, la invasión de la pared, el sitio del tumor y el estadio de la enfermedad, y con ellos elaboraron por regresión múltiple de Weibull una puntuación que determinó tres estratos con pronóstico diferente: >7 puntos, <30% de supervivencia; 3,6-7 puntos, 30-69% de supervivencia, y <3,6 puntos, más del 70% de supervivencia a los 5 años).
- El grupo de sujetos que se utilice para establecer un pronóstico debe ser lo más estable posible. Los abandonos, falta de respuesta, etc, pueden sesgar el pronóstico, no pudiendo generalizarlo a la población diana inicial.
- Si el estudio se realiza con una clase determinada de enfermos, no pueden generalizarse los pronósticos a todo el espectro de la enfermedad. Por ejemplo, el pronóstico de tener infección hospitalaria en enfermos ingresados en una UCI neonatal varía inversamente según el peso al nacer; por lo cual, si calculásemos una incidencia global (promedio de todos los ingresados) de esta complicación, estaríamos subestimando el riesgo de los neonatos con menos peso al nacer.
- Problemas para establecer un buen pronóstico en una serie de datos. Nos basamos en un estudio de cohortes, sólo que el foco de nuestra atención no estará en definir los factores de riesgo, sino los desenlaces de la enfermedad. Por ello, el estudio puede tener los sesgos típicos de este tipo de diseños:
- Sesgos de selección o de referencia. Si los individuos difieren en la gravedad de la enfermedad, los grupos ya no son comparables desde el inicio del estudio.
Esto suele ocurrir en estudios efectuados en hospitales altamente especializados o de referencia. Por ejemplo, supongamos que la prevalencia de neumococos resistentes a los antibióticos penicilánicos en nuestra población sea del 10% en invierno. Si estudiásemos una muestra de 200 casos de infección bucofaríngea, tendríamos 20 casos con dicha resistencia. Pero si en lugar de realizar el estudio poblacional nos basamos en los datos de hospitales donde sólo acude el 30% de los 200 casos, es decir, 60 que han evolucionado mal, etc, entonces, en esta cohorte truncada podemos obtener que 19 casos tienen resistencia a los penicilánicos y 41 permanecen sensibles, ya que no hemos podido observar los 140 casos (1 resistente y 139 sensibles) que curaron con atención primaria. Como consecuencia de este sesgo podríamos concluir que los neumococos se están haciendo muy resistentes en España, pues el 30% de las cepas estudiadas (en el hospital) presentan resistencia a los penicilánicos, lo que debe hacer cambiar la terapia de estas afecciones. Esto podría ser verdad en los enfermos hospitalizados, pero sería un error en atención primaria. - Sesgo de migración o abandono del estudio. Si son muy numerosos los abandonos o si se hacen de forma no aleatoria en los distintos estratos de gravedad, se produce un sesgo. Esto es relativamente frecuente si tenemos en cuenta que las razones de abandono del estudio (muerte, recuperación, efectos secundarios del tratamiento instituido, etc) están fuertemente asociadas a un pronóstico concreto más que al resto.
También puede haber un problema de migración entre las cohortes seguidas. Por ejemplo, los pacientes hipertensos con tratamiento farmacológico pueden abandonarlo y hacer solamente dieta, como la cohorte en la que sólo se realiza esta clase de intervención. Esto reducirá artificialmente la diferencia entre los dos grupos.
Otro ejemplo de migración entre las cohortes seguidas se origina cuando se clasifica la enfermedad de forma diferente en dos épocas, y luego se pretende valorar los cambios observados como diferencias debidas al diferente tratamiento realizado. Así, Feinstein et al. detectaron que se produjo este sesgo al comparar la supervivencia a los 6 meses de pacientes con cáncer de pulmón tratados desde 1977 con la que tenían los enfermos tratados entre 1953 y 1954. ¡La supervivencia había aumentado, tanto en su conjunto como por subgrupos según los estadios de la enfermedad! Pero la realidad era menos favorable, puesto que se había producido migración de estadio, por la diferente resolución de los instrumentos diagnósticos en cada época. En la tabla 21-2 se representa un ejemplo hipotético de este sesgo por migración, en el que parece haber una reducción de letalidad a la mitad (comparando el año 2006 con el año 1986) en el estadio I, así como de un tercio en los estadios II-III, etc, cuando en realidad se seguía con la misma letalidad que en el primer período, pero hubo una asignación a un estadio diferente en 100 enfermos, debido a los avances diagnósticos de la época. Es por ello necesario tener en cuenta este sesgo antes de atribuir una mejoría en el pronóstico a un tratamiento. - Sesgo de detección. Al insistir más en la búsqueda de un determinado efecto, cuando se sabe que pertenece a una cohorte y no a otra (ej. efectos secundarios por toma de medicamentos, cuando se insiste más en las preguntas que detectan estos efectos en el grupo que más consume dichos productos).
Es necesario controlar estos sesgos.
- Sesgos de selección o de referencia. Si los individuos difieren en la gravedad de la enfermedad, los grupos ya no son comparables desde el inicio del estudio.
- Comunicación de resultados. Para hacer un buen pronóstico, siempre es interesante reunir el máximo de información en un solo dato, por ejemplo:
- Porcentaje de supervivencia a los 5 años.
- Porcentaje de casos fatales o letalidad (asumiendo que el tiempo de observación es suficiente para que ocurran estos desenlaces).
- Respuesta al tratamiento (porcentaje de pacientes que mejoran tras la intervención).
- Remisión (porcentaje de pacientes cuya enfermedad ya no es detectable).
- Recurrencias (porcentaje de pacientes que recaen en la enfermedad tras un período libre de ella).
- Mediana de supervivencia. Tiempo en el que ha muerto la mitad de la población seguida (es más interesante que la media, ya que ésta se ve más afectada por los datos muy extremos).
Este tipo de comunicación de resultados tiene la ventaja de la simplicidad, la facilidad de información y retención en el oyente, etc, pero también puede inducir a equivocaciones al tratarse de una información muy sucinta. Así, podemos comparar tres series de enfermos con un 10% de supervivencia a los 5 años, pero su significado será distinto si en la primera serie el grupo de supervivientes desciende lentamente hasta alcanzar el 10% en el quinto año; en la segunda, el descenso es muy rápido pero los que sobreviven tras el primer mes ya pueden considerarse curados pues se mantiene en torno al 10%, y en la tercera, al contrario, en los 4 primeros años se mantiene una gran supervivencia que luego cae en picado, para alcanzar la cifra del 10% a los 5 años. Por ello, muchas veces es necesario presentar una información más detallada, por medio de curvas de supervivencia o de árboles pronósticos.
| Estadio | Años | |
|---|---|---|
| 1986 | 2006 | |
| I (metástasis no detectables) | No metástasis (letalidad 10%) Micrometástasis (letalidad 30%) | No metástasis (letalidad 10%) Micrometástasis (letalidad 30%) |
| II-III (metástasis detectables) | Micrometástasis (letalidad 30%) Macrometástasis (letalidad 80%) | Micrometástasis (letalidad 30%) Macrometástasis (letalidad 80%) |
| I (metástasis no detectables) | No metástasis 100 (10 mueren) Micrometástasis 100 (30 mueren) | No metástasis 100 (10 mueren) Micrometástasis 0 (0 mueren) |
| II-III (metástasis detectables) | Micrometástasis 0 (0 mueren) Macrometástasis 100 (80 mueren) | Micrometástasis 100 (30 mueren) Macrometástasis 100 (80 mueren) |
Curvas de supervivencia
En las curvas de supervivencia puede observarse el porcentaje de enfermos que sobreviven en cada momento de observación, y todo ello corrigiendo el problema de los abandonos por muerte o pérdida de seguimiento. Con este método se obtiene la probabilidad condicional de sobrevivir al final de un intervalo, habiendo entrado vivo al comienzo de éste. Pero estas curvas también pueden aplicarse a otros desenlaces distintos de la muerte, como primer reinfarto de miocardio, recurrencia de cáncer, infección hospitalaria, etc, con lo que se obtiene la probabilidad de no tener ese problema de salud al finalizar el intervalo estudiado.
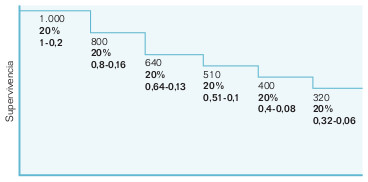
Se suele basar en cálculos de incidencia acumulada a partir de la densidad de incidencia, bien en intervalos fijos de tiempo, bien en intervalos variables, como son los que se producen cada vez que exista el evento investigado (muerte, recidiva, etc). Los sujetos perdidos durante el seguimiento se denominan «censurados» y participan en el conjunto de personas-tiempo, hasta que se pierden (fig. 21-2). La representación gráfica de estas curvas es una especie de escalera, pero si el número de escalones es muy grande, se aproxima a una curva, de donde les viene el nombre. La interpretación correcta de estas curvas debe tener en cuenta lo siguiente:
- El eje vertical representa la probabilidad que tienen de sobrevivir los miembros de una cohorte hipotética, no de una cohorte actual.
- Los puntos son estimaciones (según los datos de que se dispone) de la probabilidad de sobrevivir los miembros de una cohorte, pero la precisión de estas estimaciones depende del número de observaciones sobre las que se hace. Así, las mejores estimaciones ocurrirán en la parte izquierda de la curva, donde se sigue a más pacientes en riesgo, mientras que en la parte derecha de la curva, tras haberse producido abandonos, muertes, etc, su precisión será mucho menor.
- En las enfermedades en las que la mayoría de los sujetos estudiados experimentan el evento de interés (muerte, recurrencia, etc), las curvas suelen tener una pendiente muy fuerte al principio y luego decrecen lentamente. Pero esto último no se debe confundir con una disminución de la probabilidad de producirse el evento, ya que al haber pocos individuos, la incidencia acumulada (incidencia del intervalo anterior multiplicada por la de este intervalo) varía poco y da la falsa impresión de disminución de la pendiente.
- Debería incluirse en ellas el número de pacientes en los intervalos clave en el seguimiento, para que el lector pueda calcular, si lo desea, los límites de confianza de esos porcentajes.
- Las curvas de supervivencia pueden compararse por distintos métodos, como Logrank, que realiza un test de chi al cuadrado, o bien mediante el test de Gehan (generalización del test de Wilconson), o por el test de Breslow (generalización del test de Gehan a varios grupos), o por el método de Cox, que permite controlar simultáneamente diversos factores de confusión. Se basa en el cálculo de tasas instantáneas de un evento (muerte, fallo en un tipo de prótesis, etc) y se supone que la razón de estas tasas es constante en el tiempo del estudio (debe verificarse esta premisa antes de aplicarlo). Esta técnica permite no sólo calcular el porcentaje de muertos según tengan o no diversas características (ej. porcentaje de muerte tras una quemadura según la edad, superficie corporal quemada, profundidad, patología previa, rapidez en la intervención quirúrgica, etc), sino que también determina la odds ratio de cada uno de estos factores de riesgo incluidos en la ecuación, después de controlar el efecto de los demás.
Árboles pronósticos
En los árboles pronósticos se representan las distintas posibilidades de evolución y sus probabilidades respectivas.
Estos árboles pueden trazarse después de calcular las probabilidades correspondientes, sin necesitar una casuística muy grande, por regresión logística, método que además nos permite controlar un gran número de factores de confusión que influyen en la evolución de la enfermedad.
También es posible ofrecer sólo la fórmula de regresión, dejando libertad al lector para calcular sólo las «ramas» que le interesen.
Por ejemplo, la mortalidad por infarto de miocardio depende, según el estudio de Framingham, de varios factores, como presión arterial sistólica (PAS), tabaquismo, hipertrofia ventricular, intolerancia a la glucosa, edad y colesterol, pero si quisiéramos trazar en un árbol las múltiples ramas, eso sería difícil. En consecuencia, su fórmula permite calcular el riesgo de infarto en un grupo de sujetos, según sus características, sin la necesidad de obtener la probabilidad de todas las combinaciones posibles de esos factores pronósticos. O también, en lugar de la fórmula, nos pueden presentar una serie de puntuaciones de las que se obtiene el pronóstico del suceso objeto de estudio, como han hecho con los datos de este estudio de Framingham. Si un sujeto tiene PAS 170 (7 puntos), fuma (4 puntos) y su colesterol es de 225 con 50 años (25 puntos), suma 36 puntos, lo que equivale a una probabilidad de infarto de 14% en los 5 años siguientes.
Cálculos semejantes también nos pueden ayudar a establecer la mejor conducta terapéutica, dado el tipo de enfermo que tenemos (ej. si la probabilidad de morir es muy alta, se puede intentar una terapia más agresiva, o al contrario, sólo de cuidados paliativos, etc).
Más adelante en este capítulo se describe la aplicación de estos árboles a la toma de decisiones clínicas.
Utilización de pronósticos publicados en la bibliografía médica
A veces no disponemos de casuística suficiente para construir nuestros propios pronósticos, y hemos de recurrir a los publicados por otros autores, que en la mayoría de las ocasiones son de otros países, con una casuística que no siempre es similar a la nuestra, por lo que sus conclusiones no siempre pueden servirnos. En las siguientes líneas se dan una serie de consejos prácticos para la lectura crítica de estos artículos, siguiendo a Sackett (1994), a partir de una serie de preguntas que nos debemos hacer al enjuiciar estos artículos:
- ¿Se reunió una cohorte al comienzo del estudio? Es decir, se ha incluido a todos desde el momento inicial de su enfermedad, de tal manera que los que fallecieron o se recuperaron pronto también estén incluidos, lo mismo que los que siguen enfermos.
Si esto no se cumple, como suele pasar al realizarse estudios retrospectivos, el pronóstico aparecerá más sombrío de lo que realmente es, ya que se han eliminado todos los que curaron pronto, que suelen ser más que los que murieron precozmente y también fueron excluidos; pero también puede ocurrir lo contrario, si la mortalidad es grande en los primeros momentos del estudio y no se recogieron bien todos los casos, el pronóstico parece más favorable de lo que será en realidad. - ¿Se describió adecuadamente la forma de selección de los enfermos para ingresar en la muestra? Esto es muy importante si queremos generalizar a nuestros enfermos los resultados del trabajo que leemos (valorar si eran de atención primaria o de un hospital y la clase de éste, es decir, docente o no, o bien si procedían de una UVI, etc). Así, al describir cómo variaba la frecuencia de convulsiones no febriles, después de tener una convulsión en estado febril se halló que variaba nada menos que de 1,5 a 58%, y todo dependía del lugar donde se realizó el estudio, pues las convulsiones febriles pueden ser motivo de ingreso hospitalario, y por ello, en estos casos puede producirse un tremendo sesgo de selección, puesto que los niños ingresados no son similares a los pacientes visitados en atención primaria, ya que tenían otros factores de gravedad añadidos, que los hacían no comparables.
Además de los criterios de selección de enfermos, nos servirán todos los datos del estudio sobre edad, sexo, factores de gravedad, etc, para poder decidir si nuestros pacientes podrían parecerse o no a los del trabajo que estamos leyendo. - ¿Se realizó un seguimiento completo? Siempre hay pérdidas en la cohorte inicial, pero si éstas son muy cuantiosas, puede quedar invalidado el estudio. Una estrategia para valorar si es importante el número de pérdidas o no consiste en calcular el «peor» y el «mejor» resultado posible (es decir, si todos los sujetos perdidos hubiesen enfermado o bien si todos hubiesen sanado). Si los datos calculados no varían mucho respecto de los que se presentan con los sujetos estudiados, podremos aceptar el resultado. Por ejemplo, tengamos 100 enfermos, de los que se han seguido 90 y se perdieron 10. De los seguidos, curaron el 70% (63) y recidivaron el 30% (27). Podemos establecer dos supuestos: los 10 perdidos curaron (mejor resultado posible), entonces el porcentaje final de curación fue de 73% (63 + 10 de los 100). Pero si los perdidos recidivaron (peor resultado posible), el porcentaje de casos con mala evolución ascendería al 37% (27 + 10 de los 100).
- ¿Se utilizaron criterios objetivos para los resultados? Si no se definen claramente los criterios de «mejoría», etc, no podremos saber si el resultado corresponde o no con lo que pensamos de dicho tema, y nos será poco útil para extrapolarlo a nuestros enfermos.
- ¿La evaluación del resultado fue a ciegas? Para evitar sesgos inconscientes como los de sospecha diagnóstica o sospecha de exposición.
- ¿Hubo un ajuste adecuado por factores pronósticos? Por ejemplo, mediante un método adecuado de ajuste. También puede valorarse esto si los resultados se han validado en una muestra diferente de la inicial, de la cual se obtuvieron los factores pronósticos, o bien si había suficientes pacientes para que los ajustes originen «modelos estables». Como regla simple, se recomienda que haya, como mínimo, 10 pacientes por factor controlado.
Aplicaciones del pronóstico
- Mejora de los índices de epidemiología clínica. Si estratificamos a los enfermos por índices pronósticos, la medición de resultados de una prueba diagnóstica, evolución de la enfermedad, etc, será más objetiva.
- Mejora en la evaluación de profilaxis y tratamientos. Por ejemplo, al considerar la infección de una herida posquirúrgica, una frecuencia de infección del 5% en cirugía limpia será considerada alta, mientras que en cirugía sucia sería óptima, y esto nos indicaría que deberíamos investigar cómo se realizó la limpieza prequirúrgica, lavado de manos del equipo que intervino y profilaxis antibiótica periquirúrgica, o si la cirugía limpia fue con implantes, etc. De forma similar, cuando se vaya a hacer una aleatorización para asignar tratamiento o placebo, debería estratificarse previamente por pronóstico, ya que, de lo contrario, el azar puede actuar en nuestra contra si los dos grupos no son muy numerosos.
- Mayor objetividad en el consentimiento informado por parte del enfermo.
- Mejora de la relación médico-enfermo y disminución de problemas legales, facilitando todo ello la toma de decisiones.
##Análisis de decisión en la práctica médica: Introducción y técnicas
«La naturaleza es probabilística. La información, incompleta. Los resultados, limitados. Las decisiones, inevitables.» – H. S. Frazier, Universidad de Harvard, 1980
El análisis de decisión clínica es una metodología científica que tiene como objeto sistematizar, de forma estructurada, las opciones disponibles para la toma de decisiones en la práctica clínica. Se trata de intentar evitar el error sistemático asociado a variables de subjetividad o inexperiencia personal y minimizar el error aleatorio al que se ve sometido cada proceso de decisión, dotando de cierta seguridad y precisión un proceso que por otro lado nunca estará exento de un relativo grado de incertidumbre.
La metodología del análisis de decisiones se desarrolló como un método para ayudar a los clínicos a tomar decisiones sobre pacientes individuales, de cara a mejorar la calidad de dicho proceso, y consiste en una herramienta gráfica y numérica que facilita tomar una decisión compleja, al objetivar de forma comparativa las diversas alternativas posibles (diagnósticas, terapéuticas, etc) y al asignar explícitamente valores cuantitativos tanto a las probabilidades de los eventuales cursos clínicos como a las utilidades de los eventos derivados de ellos.
Podemos hablar de dicotomías en la tipología de decisiones alternativas a las que un clínico puede enfrentarse, aunque hay que decir que en las situaciones reales la mayoría de los casos representan combinaciones de distintos tipos:
- Decisiones con certeza o con incertidumbre. Las primeras son aquellas en las que conocemos la probabilidad de acertar, y ésta es alta; lo contrario es incertidumbre.
- Decisiones simples o complejas. Las primeras son aquellas en las que sólo influye un factor; en las segundas influyen múltiples factores.
- Decisiones operativas o estratégicas. Las primeras son concretas y afectan al presente; las decisiones estratégicas afectan a más dimensiones y tienen consecuencias sobre el futuro del servicio.
- Decisiones sin o con riesgo, según se haga en ambiente de razonable certeza o clara incertidumbre. Para la toma de estas decisiones, es necesario conocer la actitud del individuo ante el riesgo; así puede darse tendencia al riesgo (buscador de riesgos) o aversión al riesgo.
De forma complementaria, dependiendo del ámbito en el que centramos el análisis de decisión en clínica, podemos hablar de tres grandes dimensiones:
- Decisiones sobre el tratamiento clínico de un enfermo concreto.
- Decisiones sobre el tratamiento de grupos de enfermos caracterizados por un mismo problema de salud o enfermedad; es decir, sirve para desarrollar protocolos o guías de práctica clínica.
- Decisiones sobre la organización de la asistencia sanitaria.
Para la toma de decisiones clínicas, actualmente se utilizan varias técnicas: el análisis de umbral, los diagramas de influencia y el árbol de decisión. Aunque la tercera es la más utilizada (y la abordaremos con mayor detalle), a continuación se describen las tres técnicas de forma sucinta:
Análisis de umbral
Esta metodología se basa en identificar un valor crítico de los parámetros que queremos determinar, por encima o por debajo de los cuales las decisiones que hay que tomar ante una situación clínica pueden variar. El umbral de decisión podemos definirlo como el nivel de probabilidad en el que el beneficio esperable de tomar una decisión es equivalente al de no tomarla (o al de tomar una alternativa). Se conoce también como nivel de indiferencia. Las decisiones generadas con este método permiten considerar también el grado asociado de certidumbre diagnóstica, lo que posibilita su aplicación a situaciones relativamente comunes en clínica en las que, desconociéndose o dudándose sobre la presencia de la enfermedad, pueden plantearse distintas alternativas: no tratar, solicitar más información (nuevas pruebas antes de tratar) o tratar sin someter al paciente a nuevas pruebas (tratamiento empírico).
Diagramas de influencia
Los diagramas de influencia son la alternativa gráfica de los árboles de decisión (que se describirán a continuación).
Estos diagramas están constituidos por estructuras gráficas que representan los diferentes elementos que intervienen en una situación de toma de decisiones, incluyendo la secuencia en la que ellos se presentan. El objetivo de estructurar un problema con diagramas de influencia permite tomar la decisión que genere la mayor ganancia esperada (utilidad). A continuación se exponen las distintas formas gráficas utilizadas en el diseño de los diagramas:
- Rectángulo. Representa una variable que está bajo el control de quien toma la decisión y muestra las alternativas disponibles. A esta representación se le llama «nudo de decisión» y, generalmente, corresponde a un verbo (tratar, ingresar, operar, etc).
- Óvalo. Corresponde a variables aleatorias y representa un evento que depende del azar, relevante para el problema de decisión. Éstos son eventos a partir de los cuales se generan varias alternativas probabilísticas, fuera del control de quien está tomando la decisión. Corresponden a los nodos de azar o probabilísticos.
- Doble óvalo. Representa ya sea un valor constante, ya sea un valor que se puede calcular a partir de los valores de los nodos predecesores. Debido a que en cualquiera de los dos casos su valor puede establecerse con certeza, a estas representaciones se les llama «nodos determinísticos».
- Hexágono. Representa medidas del valor que se asigna a un desenlace dentro de un proceso de decisión. La medición de este valor se hace en términos numéricos y se denomina «utilidad». Por esta razón se denominan «nodos de utilidad o de valor».
- Conectores. Son flechas que sugieren influencia (conector de influencia) o flujo de información entre elecciones, eventos probabilísticos o consecuencias (conector de información). Los conectores de información se representan mediante líneas quebradas. Las flechas no deben generar circuitos reverberantes, es decir, el sentido de las flechas nunca permite devolverse a un paso previo (son modelos no cíclicos o unidireccionales).
Árbol de decisión
Para ilustrar esta técnica, usaremos el siguiente ejemplo. Atendemos en nuestra consulta a un varón de 65 años que presumiblemente presenta una enfermedad que llamaremos «cudicia» (Rodríguez Artalejo, 1990). Se trata de una enfermedad metabólica degenerativa que afecta por igual a ambos sexos y cuya frecuencia aumenta con la edad. Sus formas clínicas más graves pueden causar la muerte por afectación de la función hepática, renal o digestiva. En nuestro caso, ha comenzado de manera violenta, con notable alteración del estado general y manifestación sobre todo digestiva en forma de dolor abdominal e intensa diarrea. El diagnóstico se basa en la anamnesis, el examen físico y, entre otras exploraciones complementarias, un enema opaco en el que se observa inflamación y úlceras en la mucosa, especialmente en el colon izquierdo.
El médico se plantea lo siguiente: además de las medidas de soporte general del enfermo, hay dos actitudes terapéuticas posibles no protocolizadas:
- el tratamiento farmacológico con Eustin, o
- la colectomía parcial.
¿Por cuál nos inclinamos? Para decidir esto, construiremos un árbol de decisión. Esta técnica sigue una serie de pasos secuenciales (tabla 21-4):
- Crear un árbol de decisión o mapa de todos los posibles cursos de acción a nuestro alcance (ramas de árbol) y de sus consecuencias. En nuestro caso sólo disponemos de dos posibles cursos de acción: el tratamiento farmacológico con Eustin y la colectomía parcial. Ésta es la única decisión que tomamos y que representamos por un cuadradito vacío que recibe el nombre de nudo de decisión (fig. 21-3). A partir de aquí, el árbol funcionará de forma autónoma de nuestra voluntad, pero dependiente del resultado del tronco o rama anterior.
Si el enfermo recibe Eustin, es posible que se cure totalmente de la enfermedad, que presente una cierta mejoría, o bien que, desgraciadamente, muera por causa de la «cudicia» (fig. 21-3). Son los tres posibles resultados de la administración del Eustin. Sin embargo, el médico no controla estos resultados una vez administrado el fármaco. Dependen en cierta manera del azar. Por este motivo, delante de ellos se coloca un círculo vacío que recibe el nombre de nudo de azar.
Si optamos por la cirugía (colectomía parcial), es posible que acabemos la operación con una anastomosis colónica terminoterminal si la porción de intestino resecado no es muy importante. Si, por el contrario, el intestino resecado es amplio o afecta al recto, habrá que hacer una colostomía. La realización de la colostomía depende de elementos que el médico no controla en el momento en que decide optar por la cirugía, ya que las imágenes del enema opaco no son suficientemente informativas de la afección intestinal. Sólo lo sabrá en el momento de la operación y por eso se coloca previamente un nudo de azar (fig. 21-3). Finalmente, las consecuencias de la colectomía parcial son las mismas que las del tratamiento con Eustin, es decir, curación, mejoría o muerte por la enfermedad, a las que se añade la posible muerte durante la operación quirúrgica. Estas consecuencias dependen también de la suerte, por lo que van precedidas de un nudo de azar.
- Asignar probabilidades a todas las ramas del árbol de decisión. Se calculan probabilidades para todas las ramas que surgen de un nudo de azar. Estas probabilidades se obtienen de la bibliografía científica. En algunos casos se puede carecer de estudios que den valores de probabilidad para todas las ramas del árbol. De esta forma se identifican líneas prioritarias de investigación. Sin embargo, como obviamente queremos llegar a una solución al dilema de cómo tratar a nuestro enfermo antes de que se realicen tales investigaciones, sustituiremos los valores empíricos de probabilidades por suposiciones razonables que hacemos nosotros.
La figura 21-3 presenta los valores de probabilidad que hemos elegido para todas las ramas del árbol. Se ha asumido que ambos cursos de acción, el Eustin y la colectomía parcial, con colostomía o sin ella, son razonablemente efectivos, y que, por lo tanto, las probabilidades de curación y mejoría resultan muy superiores a las de muerte. Además, se ha supuesto que el curso clínico de la cirugía es idéntico cuando se realiza colostomía y cuando no, y que este curso es, en general, más favorable cuando se practica cirugía que cuando se administra tratamiento farmacológico. Finalmente, se asume que se hará colostomía sólo en un 20% de los casos sometidos a cirugía.
Terminamos este paso con una llamada de atención. La suma de las probabilidades de todas las ramas de un nudo de azar ha de ser 1. Significa que todas las ramas suponen sucesos colectivamente exhaustivos. Además, deben ser mutuamente excluyentes.
- Asignar un valor o utilidad a cada una de las consecuencias de un curso de acción. Las decisiones en medicina se caracterizan por dos hechos: la incertidumbre derivada de cada posible curso de acción y el grado de deseo, preferencia o valor que atribuimos a las consecuencias de cada curso. Ambos tratamientos, tanto el farmacológico como el quirúrgico, pueden ir seguidos de la curación, la mejoría o la muerte. La incertidumbre sobre cada una de estas consecuencias se expresa a través de la probabilidad que el médico asigna a cada rama del árbol. Es un trabajo esencialmente técnico que el médico debe realizar. Sin embargo, la elección definitiva del curso de acción debe tener en cuenta también las preferencias que, por cada una de sus consecuencias, tenga el que las va a experimentar, el enfermo. De esta forma se incorpora, por parte del enfermo, un elemento subjetivo a la toma de decisión clínica.
La medida de las preferencias del enfermo para cada una de las consecuencias de los cursos de acción se llama utilidad. A mayor preferencia, mayor utilidad. Las utilidades suelen expresarse en una escala que va del 0 al 1. En la figura 21-3 aparecen las utilidades o preferencias que nuestro enfermo ha expresado para cada una de las consecuencias o resultados del árbol. La utilidad de la curación es siempre superior a la de la mejoría, y la de ésta a la de la muerte. Sin embargo, nuestro paciente presenta cierta aversión a la cirugía, especialmente a la colostomía. Por eso, las utilidades de la mejoría y la muerte son más elevadas cuando se producen como resultado de la administración de Eustin que cuando se producen como resultado de la intervención quirúrgica. En este caso, además, las utilidades para la misma consecuencia son más elevadas cuando no se da colostomía que cuando ésta se da.
El bajo nivel cultural o de conciencia a veces impide al enfermo participar en la toma de decisiones expresando las utilidades. En estos casos podemos sustituir las utilidades por medidas objetivas de la efectividad de cada tratamiento o curso de acción, como la esperanza de vida. Esta información se obtendrá de la bibliografía científica.
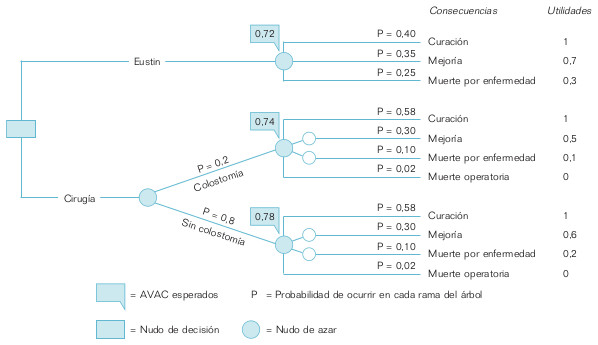
- Combinar-multiplicar las probabilidades de cada consecuencia con su utilidad. Así se obtienen las utilidades esperadas. A su vez, la utilidad esperada de cada consecuencia se suma con las de las otras consecuencias del mismo nudo de azar para obtener las utilidades esperadas de cada curso de acción. La utilidad esperada del Eustin es el resultado de (0,40 × 1) + (0,5 × 0,7) + (0,25 × 0,3) = 0,72 (fig. 21-3). De la misma forma se obtienen las utilidades esperadas de cirugía con colostomía (0,74) y sin colostomía (0,78). Por último, la utilidad esperada de la cir ugía es el resultado de (0,74 × 0,2) + (0,78 × 0,8) = 0,77 (fig. 21-3). Como vemos, se trata de un proceso que se inicia en las ramas distales del árbol y procede hacia atrás, hasta los troncos más gruesos.
Se elegirá el curso de acción que presenta la más alta utilidad esperada. Por lo tanto, en el paciente del ejemplo se procederá a realizar una colectomía parcial. En cambio, si hubiésemos usado medidas de efectividad, como los años de vida, habríamos elegido el curso de acción con una mayor efectividad esperada. La utilidad y efectividad esperadas son una medida de los beneficios que, como promedio, se derivan de cada curso de acción. La toma de decisiones basada en este procedimiento modifica sustancialmente la concepción de lo que es un buen médico. A partir de ahora, un buen médico es el que asegura los mayores beneficios como promedio para sus enfermos, y no tanto el que asegure lo mejor para un enfermo determinado. Este último objetivo es inalcanzable, dada la incertidumbre presente en toda decisión clínica complicada.
En contra de lo que parece, no se ha acabado aquí el proceso de decisión. Queda todavía un último paso fundamental (tabla 21-4).
- Comprobar que nuestra decisión sigue siendo la mejor aun produciéndose cambios razonables en la probabilidad o utilidad de cada rama del árbol. ¿Mantendríamos la decisión de practicar cirugía si la probabilidad de curarse con este procedimiento hubiese sido 0,50 en lugar de 0,58? ¿Mantendríamos esta decisión si la utilidad de la mejoría con Eustin hubiera sido 0,8 en lugar de 0,7?
Antes de reafirmarse en la decisión de operar, es necesario confirmar que las utilidades esperadas obtenidas no son sensibles, no se modifican, ante pequeños cambios en las probabilidades y utilidades. Tengamos en cuenta que las probabilidades proceden de estudios científicos que están sujetos a un cierto error, o surgen de suposiciones razonables hechas por el médico, quien, además, puede modificarlas. Esto significa rehacer todos los cálculos del árbol para cada una de estas modificaciones. Es un trabajo esencial, que recibe el nombre de «análisis de sensibilidad», pero, por desgracia, prolijo y necesitado de la ayuda de un ordenador. Existen ya varios paquetes informáticos que realizan esta tarea, como Decision Maker, DATA o una simple hoja de cálculo electrónica programada por los investigadores. Los resultados del análisis de sensibilidad también pueden dar lugar a valores umbrales de probabilidad o utilidad a partir de los que la utilidad esperada de un curso de acción cambia, es decir, pasa a ser superior o inferior a la del otro curso. Esto permite conocer mejor las «claves» del proceso de decisión en cada caso concreto.
Tabla 21-4. Pasos en la utilización de la técnica de los árboles de decisión
- Crear un árbol de decisión
- Asignar probabilidades a todas las ramas del árbol de decisión
- Asignar un valor o utilidad a cada una de las consecuencias de un curso de acción
- Combinar las probabilidades de cada consecuencia con su utilidad
- Comprobar que nuestra decisión sigue siendo la mejor, aun produciéndose cambios razonables en la probabilidad o utilidad de cada rama del árbol (análisis de sensibilidad)
Ventajas e inconvenientes de los árboles de decisión
Una ventaja de este enfoque sistemático es que no se olvida ningún curso de acción relevante. Además, se explicitan todas sus consecuencias, lo cual, junto con la valoración objetiva de las probabilidades y de la efectividad, y la valoración subjetiva de las utilidades, permite transmitir a nuestros compañeros las claves de la toma de decisión y al enfermo, participar en ella. No necesariamente tendremos que hacer lo que propone el árbol; quienes toman la decisión son el médico y el enfermo, y no el árbol, pero sí disponemos de una ayuda explícita en la que basar o justificar nuestra conducta, incluso ante demandas legales. Por último, cuantificamos y no sólo valoramos cualitativamente los pros y los contras de nuestras decisiones. Como beneficio añadido, este sistema facilita, al igual que el análisis de umbrales de probabilidad, la enseñanza de los principios de la decisión clínica.
Entre sus inconvenientes destaca lo prolijo de su realización, que debe reservarse para situaciones en que la decisión diste de ser obvia. En estos casos también será relativamente frecuente que se llegue a un empate entre las utilidades esperadas de los cursos de acción alternativos. Es difícil que los árboles incluyan todos los matices y consecuencias que están presentes en una decisión clínica. Así, nuestro árbol no incluye posibles reacciones adversas del Eustin o complicaciones de la cirugía. Por último, la elaboración de los árboles de decisión requiere bastante pericia del médico y, por lo tanto, un entrenamiento previo.
Guía para el uso de artículos que incluyen árboles de decisión
El grupo de trabajo para la medicina basada en la evidencia ha publicado unas directrices para el uso de artículos que incluyen árboles de decisión (tabla 21-5). Como siempre, hay que iniciar la lectura del artículo preguntándose por la validez del estudio y, en concreto, si el árbol construido constituye una buena descripción de la decisión que se va a tomar y sus posibles consecuencias (Richardson y Detsky, 1995a, 1995b). Obviamente, la naturaleza de la decisión y sus consecuencias pueden cambiar en el transcurso de los años, según avanzan los conocimientos médicos, por lo que debemos leer sólo descripciones actuales del problema que se estudia. El lector/usuario del artículo debe, además, asegurarse del rigor en la obtención de la información para asignar probabilidades a los resultados de cada curso de acción.
En la práctica, esta información debe obtenerse de forma similar a la utilizada en un metaanálisis, en la que se haga constar su origen y posibles limitaciones. También hay que interesarse por el origen de la información sobre las utilidades y, en concreto, saber si proceden de una muestra representativa de los pacientes o de la población general sana.
Esto permite conocer a quién pueden extrapolarse los resultados del artículo. Por último, la publicación debe contar con un análisis de sensibilidad explícito y sistemático.
Si el artículo permite responder afirmativamente a estas cuestiones, entonces tendrá sentido interesarse por sus resultados, en particular si alguno de los cursos de acción es sustancialmente superior a los demás en el análisis «basal», y si los resultados se modifican en el análisis de sensibilidad. Por «basal» se entiende el conjunto de probabilidades y utilidades (u otra medida del resultado), que los autores del artículo consideran que son los más adecuados para describir la situación ejemplarizada, y que en la publicación suelen acompañar los gráficos de los árboles de decisión. La lectura de los resultados es también el momento más adecuado para juzgar la calidad de los datos de partida para el análisis. Al igual que en cualquier otro ejercicio de síntesis de la bibliografía, la calidad de un artículo del análisis de decisión depende de la calidad de los trabajos en los que se basa. Cuantas menos probabilidades puedan estimarse con precisión a partir de trabajos de alta calidad, más débil será la evidencia utilizada en el árbol de decisión y más débiles las conclusiones que se derivan de sus resultados.
Por último, la utilidad de los resultados del artículo para el cuidado de nuestros enfermos dependerá del grado de coincidencia de las probabilidades de los eventos, y las utilidades de nuestros enfermos, con las presentadas en el artículo. Si no coinciden totalmente, podremos buscar en el análisis de sensibilidad lo que ocurre con valores de probabilidad y utilidad similares a las que creemos que tienen lugar en nuestros enfermos.
Tabla 21-5. Guía para el uso de artículos que incluyen árboles de decisión
¿Son válidos los resultados del estudio?
- ¿Se incluyeron todos los cursos de acción y potenciales resultados que son importantes?
- ¿Se utilizó un procedimiento explícito y razonable para identificar, seleccionar y combinar las evidencias existentes en probabilidades de cada resultado?
- ¿Se obtuvieron las utilidades de forma explícita y razonable a partir de fuentes creíbles?
- ¿Se valoró el impacto potencial de incertidumbres en los datos sobre los resultados del análisis?
¿Cuáles son los resultados?
- En el análisis basal, ¿alguno de los cursos de acción es mejor que el resto de forma clínicamente relevante para los pacientes? Si no es así, ¿el resultado es un empate entre los cursos de acción?
- ¿Cuál es la calidad de los datos usados en el análisis?
- ¿Podrían las incertidumbres en los datos de partida modificar los resultados del análisis?
¿Serán de utilidad los resultados para el cuidado de mis pacientes?
- ¿Se ajustan los estimadores de la probabilidad de los resultados a las características de mis pacientes?
- ¿Reflejan las utilidades las que hubieran proporcionado mis pacientes?
Herramientas informáticas recomendadas para realizar un análisis de decisión
Aunque los procedimientos de cálculo que se ejecutan en un análisis de decisión son relativamente sencillos, hoy en día tiene poco sentido realizar esta tarea de forma manual dado que existen programas informatizados que nos permiten realizar esta labor de forma más rápida y precisa.
A continuación exponemos programas informáticos disponibles en versiones de demostración que pueden ser descargados de forma gratuita desde las páginas web de sus distribuidores:
- GeNIe®. Es un programa que nos permite trabajar eficientemente diagramas de influencia. Se puede descargar desde la dirección https://www.pitt.edu/.
- DATA 3.5®. Con este programa se analizan árboles de decisión de manera ágil. Permite ejecutar varios tipos de análisis de sensibilidad. Existe una versión de demostración que se puede descargar desde la dirección http://www.treeage.com