Sesgos
Introducción
La trascendencia actual de los errores es mayor que en el pasado. Por ejemplo, en la relación tabaco-cáncer de pulmón en el estudio de casos y controles de Doll y Hill (1950), magnífico para su época, los controles hospitalarios se emparejaron 1:1 por edad y sexo a cada caso de cáncer de pulmón sin ningún criterio de restricción adicional. El tabaco provoca otras enfermedades de elevada prevalencia (como la enfermedad pulmonar obstructiva crónica) que motivan asistencia hospitalaria y, además, puede agravar otras enfermedades no causadas por el tabaco. Esto configura que dos sesgos clásicos de los estudios de casos y controles, el de inclusión y el de Berkson, estén presentes. No obstante, Doll y Hill encontraron una fuerte relación entre el tabaco y el cáncer de pulmón, posteriormente confirmada también por otros autores con diseños más adecuados. La presencia de los errores mencionados no impidió la identificación de la relación, pero la magnitud de la fuerza de la asociación tabaco-cáncer de pulmón es tan estrecha, que sólo la elección de controles con cáncer de laringe la hubiera hecho desaparecer.
En el presente, las asociaciones fuertes (como la del tabaco con el cáncer de pulmón) cada vez son más infrecuentes, ya que se han ido descubriendo. Es difícil que un error llegue a justificar completamente un riesgo relativo (RR) de 20, pero es fácil que sea responsable de un aumento de riesgo del 50% (RR = 1,5). Hoy se debate, por ejemplo, si los errores justifican que la terapia hormonal sustitutiva (THS) en la menopausia aumente un 30-40% el riesgo de cáncer de mama. Esto obliga a una mayor escrupulosidad en la investigación.
Concepto
Last define el sesgo como:
«toda desviación de la verdad que se produce en los resultados o en la inferencia de éstos, o los procesos que producen tal desviación. Cualquier tendencia en la recolección, análisis, interpretación, publicación o revisión de los datos que pueden conducir a conclusiones que son sistemáticamente diferentes de la verdad».
El error puede ser sistemático o no. Un ejemplo de error sistemático sería el esfigmomanómetro que midiese siempre 10 mmHg de más. Si se conoce, no invalida el instrumento, simplemente hay que tenerlo en cuenta. Son más frecuentes los sesgos no sistemáticos. Por ejemplo, en un estudio de casos y controles de malformaciones congénitas, las respuestas que dan las madres de los casos no tienen por qué ser igual de válidas que las que ofrecen las madres de niños normales.
La validez interna de un estudio se refiere a la inferencia realizada sobre la población elegible. La validez externa se interesa por la extrapolación de los resultados desde la población de estudio a otras poblaciones. Por ejemplo, en el estudio de cohortes de los adventistas californianos sobre el estilo de vida y las enfermedades crónicas, la validez interna plantea si es verdad que el estilo de vida saludable es un factor protector para el cáncer en los adventistas californianos, mientras que la validez externa cuestiona si eso no es sólo aplicable a los adventistas californianos, sino también a otros adventistas, al resto de la población californiana o a los habitantes de otros países. Ha de estar claro que la existencia de validez externa presupone validez interna, pero no lo contrario.
Hay que diferenciar el sesgo del error aleatorio. El error aleatorio sucede por igual en todos los grupos y no afecta en sí a la validez interna, pero sí reduce la posibilidad de encontrar una relación verdadera entre una exposición y un efecto. Produce una menor precisión en el parámetro que se quiere medir (la sensibilidad de una prueba, el RR, etc).
Clasificación
Existen cuatro grandes grupos de sesgos:
- Sesgo de confusión, por la relación que mantienen en la población base variables con la exposición y el efecto.
- Sesgo de selección, cuando la población de estudio no representa la población diana.
- Sesgo de información, cuando el error se comete en la recogida de los datos.
- Sesgo de mala especificación, cuando el análisis es inapropiado.
Los sesgos pueden ser positivos, negativos o que cambien el sentido de una asociación. En un sesgo positivo, un parámetro alcanza un valor superior al real; por ejemplo, en el análisis entre el número de nevos y el melanoma cutáneo puede estar presente un sesgo por exceso si no se tiene en cuenta a la exposición solar; esta variable aumenta el riesgo de melanoma y favorece el desarrollo de nevos. Por el contrario, un sesgo es negativo (por defecto o hacia el nulo) cuando la estimación alcanzada por un parámetro es inferior a su valor real; por ejemplo, en la relación entre la THS y el riesgo de cáncer de mama se argumenta que las mujeres que han recibido THS tienen un riesgo basal de cáncer inferior al resto de las mujeres (el efecto de la THS sería inferior al real). La exageración de un sesgo por exceso o defecto puede conducir a un cambio de sentido en la asociación. En general, se prefieren los sesgos negativos a los positivos, pues, si a pesar del error se observa una relación entre dos variables, la verdadera asociación es aún más intensa.
Sesgo y significación estadística
La significación estadística (valor arbitrario de p < 0,05) depende del tamaño de muestra, mientras que la magnitud de error oscila entre cero e infinito. Con frecuencia se confía en la significación estadística para la identificación de factores que distorsionan la comparación entre grupos; por ejemplo, en los ensayos clínicos es habitual encontrar una tabla en la que se valora si la aleatorización ha funcionado en los grupos que se comparan, y aunque las diferencias tengan una p = 0,1-0,2 en algunas variables, si no llegan al 0,05, se ignoran. Una variable desigualmente representada en los grupos que se comparan, con independencia del valor p, puede influir en el resultado final.
Sesgo de confusión
La confusión ha recibido otros nombres, que en la actualidad han caído en desuso: paradoja de Simpson, sesgo de susceptibilidad, sesgo de especificación o asociación espuria. Cuando se calcula un RR = 2, se asume que la exposición multiplica por 2 el riesgo de los no expuestos; esto es, si los expuestos no estuvieran sometidos a la exposición, tendrían el riesgo de los no expuestos (algo que no se puede comprobar directamente). Si no es así, se dice que la relación está confundida. La confusión, ante una selección y recogida de datos correctas, es un sesgo que se encuentra en la población de referencia, producido por las relaciones que mantienen otras variables con la exposición y con el efecto que se investigan. La confusión no sólo se produce por la relación que mantienen entre sí las variables. Por desgracia, otros sesgos pueden dar lugar a este error: el sesgo de selección (sobre todo cuando se utilizan los criterios de restricción) o el de información por el uso de ciertos métodos (erróneos) en la recogida de los datos.
Principios de valoración de un factor de confusión
Se asume que hay tres variables dicotómicas: efecto (E+/E–), exposición (Ex+/Ex–) y un factor de confusión (F+/F–). Los criterios que hay que cumplir por F son los siguientes:
- Debe ser un factor de riesgo del efecto, independiente de la exposición diana, o una variable fuertemente correlacionada con un determinante no medido del efecto: RR/odds ratio (OR) del factor de confusión sobre el efecto es distinta de la unidad en los no expuestos (RR u ORFE|Ex – <> 1). Para que el tabaco sea un factor de confusión en la relación alcohol-cáncer de laringe, debe aumentar el riesgo de cáncer de laringe en los no bebedores.
- Debe asociarse con la exposición problema en la población de estudio. En los estudios de cohortes la OR entre la exposición y el factor extraño debe ser distinta de 1 (ORExF <> 1). En los estudios de casos y controles se valora en los controles (ORExF|E – <> 1), ya que este grupo representa a la población. En el ejemplo anterior, el tabaquismo debe asociarse con el alcohol en la población general para que cumpla este criterio.
- No debe ser una variable intermedia entre la exposición y el efecto. Si se controlara una variable de este tipo, se amortiguaría la asociación entre la exposición y el efecto, ya que se eliminaría uno de los mecanismos por los que la exposición produce el efecto. Este criterio no suele depender de los datos, sino del conocimiento causal a priori sobre el efecto en estudio. En el ejemplo anterior, el tabaco no sería factor de confusión en la relación alcohol-cáncer de laringe si el alcohol induce el consumo del tabaco. A veces este tercer criterio se relaja.
Los criterios mencionados requieren saber dos hechos que a veces no son fáciles: que una variable sea un factor de riesgo (es fácil comprobar que hay asociación, pero no tanto etiquetarla de causal) y que no sea variable intermedia. Hay una serie de situaciones en las que el desconocimiento real del primer criterio de confusión (ser «factor de riesgo») obliga al uso de la noción «asociación». En estas situaciones, en las que se cumplen los dos primeros criterios mencionados, el ajuste por éstos conduce a fuertes distorsiones. Todas tienen en común dos hechos:
- que el posible factor de confusión es una consecuencia de la exposición, sin ser intermedia por no ser un factor de riesgo del efecto, y
- que el posible factor de confusión se correlaciona con la enfermedad en los no expuestos.
Lo anterior puede producirse cuando el posible factor de confusión y el efecto son manifestaciones distintas del mismo proceso subyacente, o cuando comparten uno o varios factores de riesgo no medidos.
Por todo ello, para una valoración adecuada de la confusión hace falta un conocimiento previo de las causas del proceso en estudio (para ver si es o no una variable intermedia), habrá que hacer análisis estadísticos (para comprobar las asociaciones de los criterios 1 y 2) y tener en cuenta los problemas particulares del diseño empleado en cada situación.
Ejemplo 1. Suponga que se estudia el riesgo de tuberculosis con respecto a tener convivientes bacilíferos. Se sospecha que los resultados pueden estar influidos por el nivel de nutrición, y se estratifica por éste. Se observa que el riesgo global de desarrollar tuberculosis se multiplica por 4 cuando hay convivientes bacilíferos, y que es 8,4 en los malnutridos y de 3,2 en los bien nutridos. ¿Hay confusión? La malnutrición en los sujetos sin antecedentes de convivientes no es un factor de riesgo (incidencia en malnutridos = 5/400 = 0,0125 = incidencia en no malnutridos = 120/9.600), por lo que no es un factor de confusión, aunque haya una asociación entre la malnutrición y los antecedentes de convivientes (80% de convivientes bacilíferos en los malnutridos frente a 46% en los no malnutridos). Es de notar, además, que se aprecia una interacción entre la malnutrición y los antecedentes de convivientes: cuando hay malnutrición, la posibilidad de adquirir tuberculosis es sensiblemente superior.
Ejemplo 2. En la relación entre el consumo de anticonceptivos orales y el riesgo de cáncer de mama se plantea el papel de variable de confusión para los antecedentes familiares de cáncer de mama. Globalmente no se aprecia ninguna relación (RR = 1,3), pero, tras estratificar por la existencia de antecedentes familiares, se observa un RR = 2 en cada estrato. Los antecedentes familiares son un factor de riesgo en las mujeres que no usan anticonceptivos orales, con un RR = 3 (cumple el primer criterio). Asimismo, se asocian con el consumo: hay un 20% de consumo en las que tienen antecedentes frente a un 80% en las que no los tienen (cumple el segundo criterio). Por último, los antecedentes preceden en el tiempo al consumo de anticonceptivos orales y no pueden ser una variable intermedia. En conclusión, se comportan como un factor de confusión, con un sesgo negativo (RR observado inferior al real).
Obsérvese que en ninguno de los ejemplos anteriores se ha empleado el concepto de significación estadística para detectar un factor de confusión. Tampoco debería depender de la investigación estadística de los propios datos obtenidos, ya que quizá no reflejen la verdadera situación de la población general, porque otros errores podrían inducir su presencia.
Control de factores de confusión
Hasta ahora se ha tratado el problema de confusión como si una sola variable fuera la responsable del sesgo. La realidad es bien distinta, y se trabaja con más de tres variables. Cuando se intentan controlar varios factores de confusión en un estudio, no se puede hacer cada uno de ellos independientemente, es necesario controlarlos todos a la vez. El primer principio que hay que mantener para poder controlar adecuadamente el sesgo de confusión es la medición correcta de las variables. La mala clasificación y la imprecisión resultante pueden provocar distorsiones importantes. Por ejemplo, una sola toma de presión arterial como indicador del nivel habitual puede motivar asociaciones no justificadas biológicamente.
El sesgo de confusión se puede controlar en el diseño o en el análisis. En el diseño puede usarse la aleatorización en los estudios experimentales. También pueden utilizarse los criterios de restricción en la selección. Por ejemplo, si se quiere analizar la relación entre alcohol y cáncer y se quiere obviar la influencia del tabaco, pueden eliminarse a todos los fumadores. Esto reduce la muestra y hay que considerar lo que es mejor, si utilizar técnicas de análisis o reducir la muestra. En el emparejamiento (matching), el grupo de referencia se elige teniendo en cuenta la distribución de uno o más factores de confusión en el grupo índice.
En el análisis existen varias alternativas: el análisis estratificado, el análisis multivariable y los métodos híbridos de los dos anteriores. En el análisis estratificado se procede de manera similar a lo expuesto en los ejemplos mencionados: se estratifica por los distintos niveles del factor que se pretende controlar y luego los distintos estratos se combinan. Existen diferentes procedimientos de combinación de estratos: la estandarización interna (teniendo en cuenta la distribución del factor de confusión en los expuestos), la estandarización externa (con la distribución en los no expuestos), el método de Mantel-Haenszel (el más usado) y la ponderación por el inverso de la varianza. Los dos primeros son auténticos métodos de ajuste, ya que eliminan la distorsión introducida por el factor de confusión. Por el contrario, el método de Mantel-Haenszel y la ponderación por el inverso de la varianza no lo son, y requieren para su uso que no haya interacción o modificación de efecto, esto es, que el RR en los distintos estratos sea uniforme.
A efectos prácticos, no se suele valorar el grado de cumplimiento de los distintos criterios de factor de confusión, sino que se comparan las estimaciones cruda y «ajustada» (generalmente por el método de Mantel-Haenszel):
$$\left ( \frac{RRajustado}{RRcrudo} - 1 \right ) \times 100$$
Si hay un cambio en la estimación superior al 10%, lo que se valora dividiendo el valor ajustado por el crudo y multiplicando por 100, se acuerda que hay confusión. Esto se ha discutido desde el punto de vista epistemológico, pero es una regla que suele funcionar. No obstante, hay situaciones en las que fracasa.
La estimación ajustada de Mantel-Haenszel es 3,5, un 12,5% inferior al valor crudo. Se concluiría que hay confusión cuando en realidad no existe y se debe a que se promedian dos estratos heterogéneos.
La ventaja que presenta el análisis estratificado es que permite un mejor conocimiento de los datos y la detección de posibles interacciones. Sus inconvenientes son esencialmente dos. El primero es que cuando se intenta controlar varias variables simultáneamente, el número de estratos resultante puede ser grande; por ejemplo, si se intenta eliminar la influencia de siete variables de confusión, cada una con dos niveles (+/–), la relación entre la exposición y el efecto se analizará en 128 estratos (= 27); si la exposición y el efecto también son binarios, el número de casillas será 512; el número de sujetos requerido para eliminar los ceros o casillas vacías es bastante elevado. El segundo inconveniente viene motivado por procesar variables continuas. El análisis estratificado obliga a la categorización de éstas, lo que puede originar confusión residual (es decir, todavía queda algún resto del sesgo de confusión). El error es tanto mayor cuanto menor es el número de categorías, es decir, es máximo cuando se dicotomiza una variable continua. Con 4-5 niveles, el error es mínimo.
Hay otras técnicas que permiten un análisis más eficiente y que obvian el inconveniente de la falta de tamaño de muestra en los estratos vacíos y el problema de las variables continuas. Son los procedimientos de análisis multivariable. Los más utilizados para efectos categóricos (presencia/ausencia) son las regresiones logística y de Cox, porque sus coeficientes (β) se transforman en OR (= eβ) y RR (= eβ), respectivamente. Al igual que en el análisis estratificado, se utiliza el criterio del 10% en el cambio de la estimación para considerar que hay confusión. Con la regresión logística en un estudio de cohortes se obtienen OR. La OR se aproxima al RR cuando la enfermedad es rara. Si la enfermedad es frecuente, la distorsión entre OR y RR puede hacer que aparezca un error importante.
En el análisis multivariable hay que cuidar tres aspectos. Primero, la elección del modelo y de las asunciones que hay que cumplir. Segundo, el control de este sesgo puede fallar si no se introducen en el modelo de rutina términos de interacción, ya que los estimadores de máxima verosimilitud (similares al método de Mantel-Haenszel) promedian estratos (en realidad no ajustan). Por último, hay que tener cuidado también con las variables continuas. Es más fácil tratarlas que en el análisis estratificado, aunque la forma en que se introducen puede plantear problemas. Si se hace tal y como se recogen, se asume una relación lineal o exponencial uniforme, etc., según el modelo elegido. Esta uniformidad no tiene por qué ser real. Es posible que haya dosis umbrales (por debajo de las cuales no se produce ningún efecto), dosis de saturación (por encima de ellas no aumenta el riesgo) y gradientes no uniformes de riesgo a lo largo de diferentes puntos de la escala. Si esto es así, para conseguir una buena modelización del efecto habría que categorizar de manera desigual e intentar reproducir la relación entre exposición y efecto. No obstante, se ha comprobado mediante simulaciones que la introducción de una variable de manera lineal es suficiente para conseguir un control adecuado de la confusión.
Se ha tratado de superar estas desventajas mediante métodos híbridos, que combinan los análisis estratificado y multivariable: la escala multivariable de factores de confusión (multivariate confounder score) de Miettinen o la estratificación asimétrica, que tiene en cuenta los posibles factores de confusión sólo en los estratos en los que existe un mínimo de información. Un procedimiento de análisis multivariable relacionado con el emparejamiento es el uso de puntuaciones de propensión a estar expuesto (propensity scores). Consisten en identificar las variables predictoras de estar en el grupo de expuestos (ej. de recibir un tratamiento). Con estas variables predictoras se construye un índice (score) que cuantifica la propensión a recibir o no la exposición. Luego, basta con emparejar a cada expuesto con un no expuesto que tenga su mismo nivel en el índice (score), o bien, alternativamente, ajustar por el índice.
Estrategia práctica en el control de factores de confusión mediante el análisis
El número de variables candidatas a ser de confusión puede ser muy elevado. Un procedimiento que se observa con mucha frecuencia es que los investigadores realizan un cribado de éstas con un criterio de significación estadística (p < 0,05 o 0,1) y todo factor que en el análisis bivariable muestre una p inferior a la establecida pasará a formar parte de las variables candidatas a ser introducidas en el análisis multivariable. Si se procede así, se asume que el sesgo de confusión siempre es positivo (valores de RR mayores a los reales) y no tiene por qué ser así, también puede ser negativo (valores de RR más bajos que los reales), y cuando la(s) variable(s) que oculta(n) el sesgo se controla(n) en el análisis multivariable, la asociación emerge. ¿Cómo seleccionar entonces las variables candidatas a formar parte del análisis multivariable? Hay que conocer los datos, para lo cual es bueno el análisis estratificado. Además, ayuda a detectar interacciones.
Bien es cierto que cuando se trabaja con muchas variables, un análisis estratificado puede ser muy engorroso. Esto se simplifica bastante si se tienen hipótesis de trabajo concretas y no se hacen cuentas «a ver qué sale». Aparte de esto, hay que aplicar el conocimiento existente: si una variable se ha identificado previamente como factor de riesgo, es candidata a ser de confusión. Por último, es preciso aplicar el sentido común y ver las variables que son intermedias entre la exposición y el efecto. Todo lo anterior reduce el número de variables candidatas.
A continuación se puede hacer un análisis multivariable progresivo paso a paso (en cada etapa el modelo incorpora un predictor), pero con un nivel de significación para la permanencia en el modelo elevado, superior a 0,2. Este proceso presenta varias limitaciones. La primera es que sólo trabaja con registros completos, esto es, sólo considerará a los sujetos que tengan información para todas las variables elegidas.
Si se exigen muchas variables, aunque las pérdidas en cada una de ellas sean escasas, el conjunto puede ser importante y trabajar con muestras distorsionadas que no representan al total. La segunda es que la gran limitación proviene de que el modelo puede introducir variables de ruido, motivo por el cual deben razonarse las variables sobre las que se configurará el modelo. El análisis paso a paso puede revelar predictores ocultos, variables que en el análisis bivariable no mantienen una relación significativa con el efecto.
Si el número de variables resultante de los procesos anteriores no es muy grande, se puede hacer una representación gráfica de las relaciones que mantienen entre sí las distintas variables, con la exposición y el efecto. Esto es lo que se llama un gráfico acíclico dirigido (DAG, en inglés). En él se representan las dependencias entre variables mediante flechas, y la punta de flecha indica la precedencia temporal. Suponga el esquema de la figura 14-2 en el que se analiza la posible interferencia de tres variables (A, B y C) entre una exposición y un efecto. Un camino dentro del diagrama representa una vía de relación entre variables (ej. Ex-A-C-E) y es directo cuando sigue siempre el sentido de la flecha (ej. AEx-E o B-C-E). El gráfico es acíclico porque no hay ningún camino directo que forme un círculo cerrado, y es dirigido porque la dependencia entre variables está especificada. Si hay asociación entre dos o más variables que no se puede justificar causalmente, se utiliza una línea de puntos sin flechas. Un camino entre dos variables está bloqueado si hay en su trazado un factor de «colisión» o variable en la que confluyen flechas de sentido contrario; por ejemplo, el camino Ex-A-C-B-E está bloqueado porque C actúa como factor de colisión (pero no lo sería en el camino Ex-A-C-E).
Para valorar la confusión entre Ex y E en la figura 14-2, se procede del modo siguiente. Primero, se suprimen todas las flechas que salen de Ex, ya que ninguna variable intermedia (o descendiente) de la exposición hacia el efecto sería factor de confusión. A continuación, se comprueba en el diagrama si existen otros caminos no bloqueados por los que pueda establecerse una relación no causal entre Ex y E (que se llaman de «puerta trasera»). En el ejemplo de la figura 14-2 hay tres: Ex-C-E, Ex-A-C-E y Ex-C-B-E. Hay que identificar el número mínimo de variables que interceptan todos los caminos de la puerta trasera. Según esto, la variable C está en los tres caminos, luego su control podría parecer suficiente para eliminar la confusión ya que neutraliza todos los caminos. No es así, porque C es un factor de colisión entre A y B y ajustar por él crearía una relación falsa entre A y B y abriría un camino ficticio inexistente hasta ahora: Ex-A-B-E. Esto obliga a incluir una variable adicional para controlar el sesgo de confusión, la A o la B. Por lo que la regla anterior tiene que completarse con el matiz siguiente: en el número suficiente de variables por las que ajustar, si hay un factor de colisión, debe incluirse otra variable del camino que transcurre a través del factor de colisión.
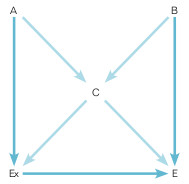
En conclusión, en el ejemplo de la figura 14-2 hay dos posibles soluciones para controlar el sesgo de confusión entre Ex y E: controlar las variables A y C o B y C.
A veces, la primera acción que se debe tomar para decidir cómo se planteará el análisis multivariable es construir el DAG para formalizar las creencias que se tienen sobre posibles relaciones causales entre variables que son candidatas a ejercer confusión. Pero los DAG pueden ser complicados si las relaciones de dependencia temporal entre las variables no se conocen lo suficientemente bien o si el número de las variables es elevado. En estas ocasiones, muy frecuentes, hay que recurrir a una aproximación heurística mediante el análisis multivariable.
A continuación, puede realizarse un modelo saturado en el análisis multivariable que incorpora todas las variables cribadas y proceder a una eliminación progresiva de aquellas que no alteran el resultado, que no cambian el coeficiente original de manera apreciable (10%). Se puede comenzar por las variables que no se relacionan de manera apreciable con el efecto (ya que no cumplen el primer criterio para ser factores de confusión), lo que se mide por el valor de la fuerza de la asociación (RR próximo a la unidad) o su significación estadística (p > 0,2). Los pasos anteriores se resumen en la tabla 14-3. Estos procedimientos descritos no son válidos cuando un factor de confusión también es una variable intermedia. En estos casos hay que recurrir al cálculo del algoritmo G o a los modelos marginales estructurales.
Sesgo de selección
En sentido estricto, este sesgo surge cuando la variable resultado que se valora (la exposición en los estudios de casos y controles, la enfermedad en los de cohortes) influye de modo diferencial en la selección de los grupos que se comparan. Se produce con más frecuencia en los estudios de casos y controles. Las fuentes posibles de este error se resumen en la tabla 14-4.
Tabla 14-3. Pasos que hay que seguir en la detección de un sesgo de confusión
- Revisar la bibliografía: identificar factores de riesgo (o protectores) conocidos del fenómeno en estudio y su posible asociación con la exposición que se valora
- Eliminar los factores de riesgo que se consideren variables intermedias entre la exposición y el efecto
- Realizar un análisis estratificado de tercera variable: por todas aquellas que quedan después del paso 2. Ayuda a detectar interacciones
- Realizar un modelo multivariable paso a paso (exploratorio) hacia delante con todas las variables candidatas, permitiendo la inclusión de variables con p < 0,2
- Realizar un gráfico dirigido acíclico
- Realizar un modelo multivariable saturado con las variables seleccionadas a partir de las etapas anteriores
- Aproximación heurística: realizar nuevos modelos sacando e introduciendo las variables del modelo saturado para retener aquellas que cambian la estimación en más de un 10% del coeficiente de la exposición con respecto al modelo saturado
Sesgos en la formación de la población de estudio
Aquí el error se puede producir por varias razones. La mala definición de la población de estudio es un error introducido por el investigador. Hay dos tipos fundamentales de base poblacional: comunitaria, cuando se origina el proceso en la población, u hospitalaria (o institucional), cuando se genera como consecuencia de la actividad asistencial. El abordaje comunitario de un proceso originado en la colectividad no suele plantear demasiados problemas; los problemas se plantean más a la hora de conseguir su aceptación. Por el contrario, sí suelen existir más dificultades cuando se hace un abordaje hospitalario de un problema comunitario. La figura 14-3 representa el esquema por el que los pacientes de un hospital pueden llegar a ser considerados candidatos a una investigación y no representar el suceso en estudio. No todos los pacientes afectados de un proceso tienen por qué sentirse enfermos; por ejemplo, una enfermedad de Parkinson en un anciano puede ser considerada simplemente algo de la vejez.
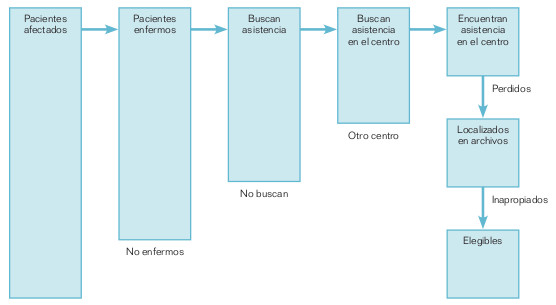
No todos los enfermos tienen por qué buscar asistencia; también influye la gravedad de la enfermedad, su capacidad de aguante, etc. No todos los pacientes tienen por qué buscar asistencia en el centro que les corresponde; las amistades, la popularidad de ciertos especialistas o la capacidad económica condicionan en gran medida adónde puede ir un paciente en busca de la solución a su problema. No todos los que buscan asistencia la encuentran, el caso puede no ser diagnosticado. Por desgracia, tampoco todos los atendidos en un centro se localizan adecuadamente en los archivos, ni todos son adecuados para formar parte de una investigación. Estos hechos pueden condicionar la falta de representatividad de una muestra y justificar por qué en numerosas ocasiones los estudios hospitalarios no coinciden con los comunitarios.
También ayuda a justificar por qué unos estudios hospitalarios difieren de otros en sus resultados.
Con independencia de lo anterior, hay que valorar los criterios de definición de la población de estudio, entre los que se incluyen los criterios de elegibilidad. Dentro de ellos se pueden incluir elementos que seleccionan una subpoblación particular, como la selección telefónica. Se puede introducir un sesgo de selección por varios motivos:
- por una cobertura telefónica incompleta, que es lo habitual en nuestro país;
- por no poder contactar con los residentes en función de variables relacionadas con la exposición, y
- cierto tipo de hogares tienen más probabilidad de ser seleccionados que otros: los que tienen más de un número de teléfono.
El uso de ciertas técnicas de diseño, como el emparejamiento, también puede motivar que la población seleccionada no represente a la elegible. Es ya sabido que el emparejamiento introduce un sesgo que se controla en el análisis, cuando es por frecuencia ajustando por las variables por las que se empareja, y con el análisis emparejado cuando es individual.
Los problemas en la extracción de la muestra que constituye la población de estudio se deben más a los sujetos que a los investigadores, aunque si la técnica de aproximación a los individuos no es correcta, también lo pueden motivar aquéllos. El sesgo más frecuente en este grupo es el de respuesta: los participantes no son similares a los que no participan. Los factores que lo determinan no son consistentes. Los sujetos que acceden a participar con mayor frecuencia son más saludables: fuman y beben menos, hacen más ejercicio, tienen una dieta más equilibrada, etc. Pero esto no es una regla, ya que también se ha documentado lo contrario.
Este tipo de errores es más infrecuente cuando se opta por una población hospitalaria que en los estudios comunitarios. Las razones son sencillas: los pacientes están hospitalizados, inmovilizados y mantienen una relación de dependencia con el personal sanitario. Por ello es más fácil muestrearlos (el universo es más limitado y con frecuencia existen facilidades informáticas) y obtener su consentimiento que en la colectividad, que es una población móvil, cambiante, sin ningún vínculo con el grupo de investigación, difícil de localizar y de enumerar en su totalidad.
Hay dos indicadores del proceso de selección que tienen que figurar en todo estudio: la tasa de participación (participantes/elegidos) y la tasa de respuesta (participantes/contactados). Cuanto más bajas sean las tasas mencionadas, mayor es la probabilidad de que exista un sesgo.
El uso inapropiado de las pruebas diagnósticas en la población puede causar un sesgo de selección, especialmente en los diseños en los que se parte de la enfermedad ya diagnosticada (como los estudios de casos y controles). Éste es un error que gradualmente merecerá más atención porque cada vez se difunden más las pruebas de cribado y por la falta de uniformidad en las recomendaciones (ej. no coinciden las recomendaciones del US Preventive Services Task Force con las de la sociedad canadiense o con las de la American Cancer Society). Con independencia de ello, hay ciertos factores que se asocian con una práctica desigual del cribado. Por ejemplo, las mujeres que van a recibir una prótesis mamaria se someten a una exploración detallada de mamas, que suele incluir una mamografía. Los casos que se detecten no contribuirán a la experiencia de cáncer del grupo, por lo que parten de un riesgo de cáncer de mama inferior al de la población general. En la evaluación de los riesgos de estas prácticas hay que tener en cuenta que el cribado se aplica de manera diferencial.
Sesgo de selección por problemas en la recogida de información
Dos son las grandes razones que pueden provocar la presencia de un sesgo de selección por una alteración en la recogida de datos:
- Las pérdidas durante el seguimiento obligan a que el análisis se restrinja a los que permanecen en el estudio y éstos no tienen por qué ser representativos de los que iniciaron la investigación: la razón de abandono puede estar relacionada con la exposición y con el riesgo de enfermedad. Son más frecuentes en los estudios comunitarios que en los estudios realizados en la clínica. En la clínica existe un mayor vínculo entre investigadores y participantes, y esto disminuye el número de pérdidas. Las razones que influyen son similares a las del sesgo de respuesta.
- Las pérdidas selectivas de información en ciertos sujetos pueden producir un sesgo de selección. Pérdidas de información escasas en cada sujeto pueden suponer alteraciones profundas en el análisis de los datos. Esto se debe a que el análisis multivariable se restringe a los sujetos en los que existe toda la información para las variables especificadas, y los sujetos en los que está presente toda la información necesaria no tienen por qué ser representativos del total seleccionado. Esto tiene una especial relevancia en el estudio de factores pronósticos con información retrospectiva procedente de la historia clínica. Normalmente, los pacientes en los que existe más información son aquellos que necesitan más estudio, y suelen ser los más graves. Por lo tanto, el análisis se centra en una submuestra peculiar de pacientes y las conclusiones obtenidas no tienen por qué generalizarse al resto de pacientes.
Control del sesgo de selección
- En la planificación del estudio (dónde tiene que hacerse) deben usarse, siempre que sea posible, exposiciones y casos de enfermedad incidentes y evitar los prevalentes; se han de aplicar los mismos criterios para la selección de los sujetos de los distintos grupos que serán comparados, y todos los sujetos potenciales deben tener los mismos procedimientos diagnósticos e idéntica vigilancia de la enfermedad.
- En la recolección de la información hay que disminuir al mínimo la no participación y las pérdidas al seguimiento; mantener un registro de todas las pérdidas y recoger la máxima información posible sobre ellas; hay que reunir tanta información como sea posible con respecto a la historia de la exposición; se ha de estar seguro de que la enfermedad se diagnostica de manera enmascarada con respecto al nivel de exposición, y que la exposición no está influida por la presencia de enfermedad.
- En el análisis normalmente es tarde. En ciertas ocasiones hay problemas a la hora de diferenciar un sesgo de selección del de confusión. Se ha afirmado que si se recogen los datos sobre las variables que introducen el error, el error es controlable. No siempre es así. Es controlable cuando los factores que afectan a la selección se miden en todos los sujetos y: a) estos factores son antecedentes de la exposición y de la enfermedad (como si fueran factores de confusión), o b) se conoce la distribución conjunta de estos factores en la población de origen y mediante el uso de técnicas especiales se puede ajustar por el error. Una condición equivalente a b) se da cuando se conocen las probabilidades de selección para cada uno de los factores que influyen en la selección.
El análisis puede tener una triple función. La primera es detectar la posible presencia de un sesgo de selección. Para ello hay que comparar las pérdidas con los restantes según ciertas características de base (estos análisis no pueden confirmar la ausencia del sesgo o estimar su magnitud) y usando los resultados del estudio, el sentido común y el conocimiento previo, tratar de deducir su repercusión. El análisis valora las pérdidas selectivas de información con respecto a algunas variables. Por último, puede realizarse un análisis de sensibilidad, y para ello habría que utilizar las probabilidades de selección de cada grupo.
Sesgo de información
Dentro del sesgo de información se incluyen todos los errores sistemáticos que se producen en el proceso de recogida de datos. Existen tres fuentes básicas de sesgo de información: la mala clasificación de la enfermedad y/o la exposición, la regresión a la media y la falacia ecológica.
Sesgo de mala clasificación
Consiste en clasificar erróneamente tanto a los expuestos como a los no expuestos, o viceversa, o tanto a los enfermos como a los sanos, o viceversa. Se puede producir por tres razones básicas:
- error en el procedimiento, que incluye los problemas de calibración de un instrumento, los problemas de memoria del sujeto en la entrevista, el uso de la historia clínica, etc.;
- error por el uso de variables sucedáneas (proxy), que intentan sustituir a la variable de interés (ej. se puede asumir como fecha de contagio de una enfermedad infecciosa el tiempo de incubación mediano desde el comienzo de la clínica, lo cual no tiene por qué ser así), y
- error en la definición de variables, por problemas de ambigüedad. Hay variables, como la clase social, que no son fáciles de definir.
Para valorar el sesgo de mala clasificación, se requiere la existencia de un criterio de verdad, que en muchas situaciones no existe. Por ejemplo, en el consumo de alcohol pueden existir parámetros (como la gammaglutamil transpeptidasa, alcoholemia) que pueden orientar acerca del consumo más o menos reciente de alcohol, pero no indican si es verdad o no la historia de consumo narrada por el individuo o la intensidad del hábito. Los errores son más habituales en la valoración de la exposición que en la de la enfermedad.
Sesgo de mala clasificación no diferencial
Cuando el grado de clasificación correcta de una variable (la enfermedad o la exposición) es la misma por los distintos niveles de otra. Por ejemplo, el sesgo de mala clasificación no diferencial de la enfermedad significa que la sensibilidad y especificidad diagnóstica es la misma en los expuestos y en los no expuestos. Produce normalmente una infraestimación del valor del RR, lo que requiere mayor tamaño de muestra para tener la misma potencia estadística. Suponga los datos de la tabla 14-5a, referentes a un estudio de casos y controles sobre consumo de alcohol y cáncer de esófago. En la realidad, sin embargo, los criterios empleados para valorar la exposición no son perfectos. Se puede asumir, por ejemplo, que la detección del consumo de alcohol tiene una sensibilidad (capacidad de identificar el consumo en bebedores) del 95% y una especificidad (capacidad de confirmar el no consumo en los que no beben) del 99%, y que estos valores son los mismos para los casos y para los controles. Esto introduce un error no diferencial. Tras la corrección pertinente, la tabla 14-5a se transforma en la tabla 14-5b: si hay 200 casos que verdaderamente beben, el 95% (sensibilidad) de ellos son detectados (200 × 0,95 = 190), a los que hay que sumar los falsos positivos obtenidos en los 800 que no beben, porque la especificidad no es perfecta (800 × 0,01 = 8); 190 + 8 = 198. En los casos no expuestos se procede de manera similar, habrá 802 realmente no expuestos (= 800 × 0,99 + 200 × 0,05 = 802).
| Exposición | Casos | Controles | OR |
|---|---|---|---|
| a) Sin sesgo de mala clasificación | |||
| Alcohol ≥ moderado | 200 | 100 | 2,25 |
| Leve | 800 | 900 | 1 |
| b) S = 0,95 y E = 0,99 para casos y controles | |||
| Alcohol ≥ moderado | 198 | 104 | 2,12 |
| Leve | 802 | 896 | 1 |
| c) S = 0,98 en casos y 0,92 en controles, E = 1 | |||
| Alcohol ≥ moderado | 196 | 92 | 2,41 |
| Leve | 804 | 908 | 1 |
De igual manera se procederá con las casillas de los controles. En la nueva tabla así configurada, el valor de la OR real es inferior al obtenido en la tabla 14-5a: 2,12 frente a 2,25.
Si se cambian en el ejemplo los valores de sensibilidad y especificidad de la detección de la exposición se comprobará que el sesgo siempre es negativo. Pero no tiene por qué ser así en las variables politómicas, e incluso puede aparecer una relación de dosis-respuesta inexistente. Es práctica común categorizar las variables continuas, generalmente en cuantiles (deciles, quintiles, cuartiles, terciles). Esta categorización conduce a una mala clasificación de la información. Aunque clásicamente se ha asumido que los errores aleatorios en la medición de una variable no relacionados con la otra producen mala clasificación no diferencial, esto no siempre es así y es perfectamente factible que ésta sea diferencial. El grado de mala clasificación en ciertas ocasiones no se relaciona con el valor de la exposición, pero cuando hay correlación entre el error y el propio valor de la exposición, se puede alterar el aserto de que la mala clasificación no diferencial siempre sesga el resultado hacia el nulo. Debería asumirse que la mala clasificación no diferencial siempre existe en mayor o menor grado en los estudios epidemiológicos.
Sesgo de mala clasificación diferencial
Cuando el grado de clasificación correcta de una variable (la enfermedad o la exposición) es diferente en los distintos niveles de la otra.
Aquí, el sentido del sesgo no es uniforme. Supóngase ahora en el ejemplo sobre la asociación entre consumo de alcohol y cáncer de esófago que la enfermedad condiciona las respuestas frente al alcohol. Por razones de simplificación se asume que la especificidad es del 100%, pero la sensibilidad es mayor en los enfermos (deseosos de colaborar), 98%, que en los que no lo están, un 92%. Corrigiendo la tabla 14-5a, en función de estos valores de sensibilidad se llega a las cifras de la tabla 14-5c. En este caso, el valor de la OR es superior al obtenido en la tabla 14-5a. Si el lector cambia los valores de sensibilidad y especificidad del caso anterior, comprobará que el sesgo puede tomar cualquier sentido. Por ejemplo, si se mantienen los valores de sensibilidad anteriores, con una especificidad del 95%, el valor de la OR será de 1,95.
La enfermedad también puede clasificarse mal, con independencia de si hay o no mala clasificación de la exposición. Si son independientes ambas malas clasificaciones, el sentido del sesgo será hacia el nulo. Pero esto no tiene por qué ser así. De hecho, es bastante probable que la mala clasificación de la enfermedad y de la exposición se correlacionen. Por ejemplo, en encuestas poblacionales los datos sobre la exposición y el efecto se recogen mediante entrevista personal en unos grupos, mientras que en otros se utiliza a informadores sucedáneos (por imposibilidad del sujeto elegido) y no es de extrañar que se correlacionen las mediciones malas. También puede producirse en los estudios multicéntricos: la aplicación del protocolo puede ser mejor en unos centros que en otros, tanto para la enfermedad como para el efecto. Si hay correlación entre los errores, el sesgo no es predecible y puede producirse por exceso.
Mala clasificación de covariables
Hasta ahora se ha planteado el problema de la mala clasificación como si sólo sucediera a la exposición y/o al efecto. Del estudio del sesgo de confusión se deduce que en una investigación hay que considerar la posible influencia de otras variables en la asociación de interés y la mala clasificación también puede afectarlas.
Las consecuencias de la mala clasificación de un factor de confusión dicotómico son que el efecto atenuante del ajuste desciende, y su consecuencia es la confusión residual; el sesgo está en el mismo sentido, pero menos corregido. Hay que señalar que grados moderados de mala clasificación pueden dificultar en gran medida el ajuste. Por ejemplo, un 10% de mala clasificación (sensibilidad y especificidad del 90%) disminuye a la mitad la reducción del sesgo de confusión en el ajuste; el ajuste es virtualmente ineficaz cuando existe un 30% de mala clasificación. Además, la distorsión no diferencial de estas variables puede producir heterogeneidad de efecto, cuando sólo había confusión. Cuando la mala clasificación no diferencial afecta a una variable de confusión con más de dos niveles, sucede algo parecido a lo comentado con una exposición politómica, la regla puede alterarse: las estimaciones ajustadas pueden ser contrarias a las esperadas.
Si la mala clasificación es diferencial, el problema se complica y el sentido del sesgo es impredecible.
Corrección del sesgo de mala clasificación
Se expondrá a continuación la corrección de sensibilidad y especificidad de la exposición y de la enfermedad no diferencial: la mala clasificación de la exposición es similar en los enfermos y no enfermos, y la mala clasificación de la enfermedad es idéntica en los expuestos y no expuestos. Además, hay que asumir que los errores de mala clasificación de ambas variables son independientes. Si se llama S y E a la sensibilidad y especificidad de clasificación de la enfermedad, y S’ y E’ a la sensibilidad y especificidad de la exposición, bajo las asunciones anteriores, se puede demostrar que los valores corregidos de las cuatro casillas son:
$$a_{c} = \frac{\left [E \left (m_{1} E’ - c \right ) - \left (1 - E \right ) \left (m_{0} E’ - d \right ) \right ]}{K}$$
$$b_{c} = \frac{\left [S \left (m_{0} E’ - d \right ) - \left (1 - S \right ) \left (m_{1} E’ - c \right ) \right ]}{K}$$
$$c_{c} = \frac{\left [E \left (m_{1} S’ - a \right ) - \left (1 - E \right ) \left (m_{0} S’ - b \right ) \right ]}{K}$$
$$d_{c} = \frac{\left [S \left (m_{0} S’ - b \right ) - \left (1 - S \right ) \left (m_{1} S’ - a \right ) \right ]}{K}$$
siendo K = (S + E - 1)(S’ + E’ -1)
Regresión a la media
Este término lo utilizó por vez primera Francis Galton en su artículo «Regresión hacia la mediocridad en la estatura hereditaria» en 1886, al relacionar la altura de los hijos con la media de sus padres. Hijos y padres tenían la misma estatura media (173 cm); sin embargo, los padres con una estatura media entre 178 y 180 cm tenían hijos con una estatura media de 176,5 cm. Galton llamó a esto «regresión hacia la mediocridad», porque era un eugenista preocupado por los problemas de extinción de las grandes familias o los buenos genes de las razas no degeneradas. Hoy se llama regresión a la media, ya que sucede lo mismo si se realiza al revés: la estatura media de los padres de hijos con estatura entre 178 y 180 cm era de 175 cm. No era un problema genético sino estadístico.
La ecuación de una recta de regresión es y = β0 + β1x, donde y es la variable dependiente y x, la independiente. El análisis de regresión estima el coeficiente de correlación r, lo bien que se ajusta la recta de regresión a la nube de puntos. Normalmente r no es perfecto y es <1. La pendiente β1 se puede calcular como psy /sx , siendo sx y sylas desviaciones estándares de x e y. Si r < 1, el cambio en una desviación estándar de x se asocia con r desviaciones estándar de y; esto es, para cualquier valor de x el valor esperado de y está menos alejado de la media de y que x de la suya. Esto es más evidente cuando se trabaja con sujetos con valores extremos y luego en este grupo se realiza una nueva determinación del parámetro. Cuanto menor sea r entre las dos determinaciones, mayor será el fenómeno de regresión a la media.
Con independencia de la regresión a la media como fenómeno estadístico está el sesgo: la tendencia a que el valor extremo de la primera medición de una variable continua se aproxime a la media de la población en mediciones posteriores. Hay muchas situaciones en las que se puede presentar. Una de las más frecuentes es en la valoración de la eficacia de los tratamientos, en el que los sujetos se seleccionan por valores extremos (colesterol elevado, presión arterial alta, etc). Se aprecia en estos casos una tendencia a que las mediciones siguientes den un valor más cercano a la media poblacional, con independencia de la eficacia del tratamiento instaurado. Hay que ser cauto cuando se relaciona la eficacia de un tratamiento en función de la gravedad del proceso, ya que se puede postular que un tratamiento es tanto más eficaz cuando más grave es el proceso, pero también es más intensa la regresión a la media. Justifica también el que los estudios iniciales acerca de la eficacia de un tratamiento o de la capacidad diagnóstica de una nueva prueba sean mucho más esperanzadores de lo que luego resultan en la realidad.
Si lo que interesa no es el nivel casual de una variable continua, sino su perfil medio basal, se puede presentar la regresión a la media cuando los sujetos se seleccionan con una sola determinación. Esto es frecuente cuando se exige que en esa determinación aislada los sujetos tengan valores iniciales muy altos o bajos. Se puede asumir que una medición aislada es válida en la medida que se basa en la fluctuación aleatoria de la medición en los sujetos. Pero no es así, ya que los sujetos con valores bajos y altos suelen estar en exceso representados y esto conduce a una valoración menor de la relación existente entre la variable y el efecto. Esta atenuación en el valor de la fuerza de la asociación reduce la potencia estadística y la fuerza a tener que elegir muestras de mayor tamaño.
Hay varios procedimientos para reducir o evitar este tipo de error. En primer lugar, se puede usar un grupo de comparación que no recibe el tratamiento experimental. En segundo lugar, la realización de varias mediciones basales y el uso de su promedio como punto de partida reduce la variabilidad introducida por el azar. En tercer lugar, se puede estimar la regresión a la media de manera separada al efecto mediante el uso de técnicas analíticas, que suponen asumir varios hechos acerca de la variabilidad del efecto en la población de origen. Por último, la regresión a la media se puede evitar si se realizan dos determinaciones antes de la intervención: una sirve para realizar la selección y la segunda, como valor basal para valorar el efecto de la intervención.
Esta aproximación elimina el sesgo si la correlación entre la primera y la segunda determinación es la misma que entre la segunda y la tercera.
Falacia ecológica
Es la mayor limitación de los estudios ecológicos. Este error se produce por la propia agregación, que obliga a asumir que la exposición de la comunidad es la que tiene cada sujeto de la propia comunidad. Cuanto mayor sea el nivel de agregación, mayor será la posibilidad de que se presente el error. Fue reconocido por primera vez por Robinson en 1950 en la sociología, que acuñó el término y proporcionó una relación matemática, sin pruebas, entre la correlación ecológica y la correlación individual en los distintos grupos. Un ejemplo frecuente para ilustrar este error es el estudio del sociólogo francés Émile Durkheim sobre el suicidio en las provincias de Prusia entre 1883 y 1890. Encontró una relación directa entre la proporción de protestantes y la tasa de suicidio. Esto no quiere decir que haya una relación entre ser protestante y suicidarse, porque lo anterior es compatible con la hipótesis de que en las regiones con más protestantes, los católicos se suicidan más, quizá por ser menos y así tener menos apoyo entre ellos, y viceversa.
Suponga el ejemplo de estudio ecológico de la tabla 14-6.
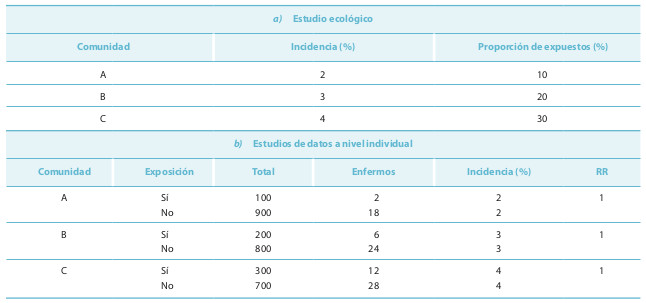
Cualquier análisis apreciaría una correlación perfecta (r = 1) entre la frecuencia de exposición y el efecto de interés, que supone un RR = 11. Los datos del estudio ecológico son compatibles con los que se encuentran en cada comunidad (tabla 14-6b). En todas las colectividades se aprecia que la incidencia de enfermedad en los expuestos y en los no expuestos es idéntica (RR = 1). En el ejemplo de la tabla 14-6 existe una relación entre la comunidad, la cifra de enfermedad y la frecuencia de exposición. También puede producirse la falacia ecológica por un factor modificador de la relación a nivel de grupos, con independencia de los factores que se muestran relacionados a nivel individual. No se debe confundir la confusión clásica con la falacia ecológica, ya que no es necesario que se produzcan las relaciones con la exposición y el efecto para que la falacia se presente. No habrá falacia ecológica si:
- las tasas de enfermedad en los no expuestos son similares en todas las poblaciones, lo que significa que no hay otros factores de riesgo distribuidos de manera diferencial en las distintas comunidades, y
- si la influencia que tiene la exposición sobre el efecto no cambia en las distintas comunidades, lo que significa que no hay modificadores de la relación desigualmente distribuidos en las comunidades.
No se necesita la condición de confusión a nivel individual para que se presente la falacia ecológica, simplemente se necesita que se asocie el factor de riesgo con el nivel de agregación.
La falacia ecológica puede cambiar el sentido de una asociación. Se utilizaron los datos del NHANES II para comprobar a nivel empírico qué era lo que sucedía a nivel individual y con diferentes niveles de agregación. Se examinaron trece pares de asociaciones (peso-talla, calorías-proteínas, raza-ingresos, etc). De manera impredecible, el análisis ecológico aumentaba, disminuía o cambiaba el sentido de la asociación observado con los datos individuales. El uso de variables adicionales ecológicas, para ajustar por ellas en el análisis multivariable, no elimina el error y puede tener como consecuencia desgraciada el que lo aumente. La estandarización de tasas tampoco la elimina. Esto limita extraordinariamente las posibilidades de controlar este tipo de error en el análisis y no favorece el entusiasmo por los diseños con datos agregados.
Para evitar la falacia ecológica, es recomendable comparar áreas que tienen una distribución similar de las covariables importantes, que sean lo más homogéneas posible, algo que se consigue con unidades más pequeñas de análisis (si es posible). Pero hay que tener cuidado, porque las unidades más pequeñas pueden aumentar la distorsión que producen las migraciones, y aumentar el fenómeno de la falacia ecológica (ya que hay más grupos), y las frecuencias de enfermedad pueden ser menos robustas si el proceso es raro.